题目内容
5.如图,两棵大树AB、CD,它们根部的距离AC=4m,小强沿着正对这两棵树的方向前进.如果小强的眼睛与地面的距离为1.6m,小强在P处时测得B的仰角为20.3°,当小强前进5m达到Q处时,视线恰好经过两棵树的顶端B和D,此时仰角为36.42°.(1)求大树AB的高度;
(2)求大树CD的高度.
(参考数据:sin20.3°≈0.35,cos20.3°≈0.94,tan20.3°≈0.37;sin36.42°≈0.59,cos36.42°≈0.80,tan36.42°≈0.74)

分析 (1)在Rt△GEB中,得到EG=$\frac{BG}{tan20.3°}$=$\frac{BG}{0.37}$,在Rt△GBF中,得到FG=$\frac{BG}{tan36.42°}$=$\frac{BG}{0.74}$,根据已知条件即可得到结论;
(2)根据(1)的结论得到FH=FG+GH=9,根据三角函数的定义即可得到结论.
解答 解:(1)解:在Rt△BEG中,BG=EG×tan∠BEG,
在Rt△BFG中,BG=FG×tan∠BFG,
设FG=x米,(x+5)0.37=0.74x,
解得x=5,
BG=FG×tan∠BFG=0.74×5=3.7,
AB=AG+BG=3.7+1.6=5.3米,
答:大树AB的高度为5.3米.
(2)在Rt△DFG中,DH=FH×tan∠DFG=(5+4)×0.74=6.66米,
CD=DH+HC=6.66+1.6=8.26米,
答:大树CD的高度为8.26米.
点评 本题考查了解直角三角形的应用-仰角、俯角问题,解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.

练习册系列答案
相关题目


 如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD,连接BD交AC于E.
如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD,连接BD交AC于E. 如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.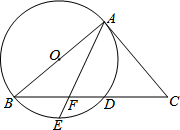 如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.