题目内容
19.从等边三角形内一点向三边作垂线,已知这三条垂线的长分别为1,3,5,则这个等边三角形的面积是$27\sqrt{3}$;.分析 作AM⊥BC,根据等边三角形的面积计算可以求得AM=PE+PD+PF,再根据等边三角形的高线长可以计算等边三角形的边长,即可解题.
解答 解:过A作AM⊥BC,则AM为BC边上的高,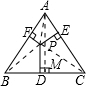
连接PA、PB、PC,
则△ABC的面积S=$\frac{1}{2}$BC•AM=$\frac{1}{2}$(BC•PD+AB•PF+AC•PE),
∴BC•AM=BC•PD+AB•PF+AC•PE,
∵△ABC是等边三角形,
∴AB=BC=AC,
∴BC•AM=BC•PD+BC•PF+BC•PE=BC•(PD+PF+PE),
∴PD+PE+PF=AM,
∴△ABC的高为:1+3+5=9,
∴△ABC的边长为:AB=$\frac{AM}{sin∠ABC}$=9×$\frac{2}{\sqrt{3}}$=9×$\frac{2\sqrt{3}}{3}$=6 $\sqrt{3}$,
故面积为$\frac{1}{2}×\frac{1}{2}×6\sqrt{3}×9=27\sqrt{3}$,
故答案为$27\sqrt{3}$;
点评 本题考查了三角形面积的计算,考查了等边三角形边长和高线长的关系,本题中求AM=PD+PE+PF是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
11.已知点A、B分别在x轴正半轴、y轴正半轴上移动,AB=4,则以AB为直径的圆周所扫过的区域面积为( )
| A. | 4π | B. | 8π | C. | 2π+4 | D. | 6π+4 |
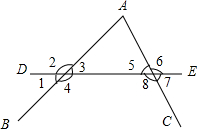 如图,直线DE截AB,AC,构成八个角:
如图,直线DE截AB,AC,构成八个角: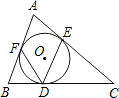 如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数. 不同的中文代表不同的数字,则“中国福州”这个四位数是1098.
不同的中文代表不同的数字,则“中国福州”这个四位数是1098.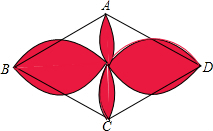 如图,四边形ABCD是菱形,AB=10cm,∠ABC=60°,分别以ABCD的四条边为直径作半圆.求图中红色部分的面积.
如图,四边形ABCD是菱形,AB=10cm,∠ABC=60°,分别以ABCD的四条边为直径作半圆.求图中红色部分的面积.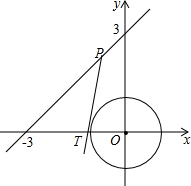 如图,在直角坐标系中,圆O是以坐标原点为圆心,半径为1的圆,直线L的方程为x-y+3=0,在L上任取一点P作圆O的切线,切点为T,则PT长的最小值是$\frac{\sqrt{14}}{2}$.
如图,在直角坐标系中,圆O是以坐标原点为圆心,半径为1的圆,直线L的方程为x-y+3=0,在L上任取一点P作圆O的切线,切点为T,则PT长的最小值是$\frac{\sqrt{14}}{2}$.