题目内容
20.解下列方程(1)4x2-4$\sqrt{2}$x+1=0
(2)(3x+2)2=(5-2x)2.
分析 (1)根据求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$解方程即可;
(2)先移项,然后利用平方差公式因式分解并解方程.
解答 解:(1)∵a=4,b=-4$\sqrt{2}$,c=1,
∴b2-4ac=(-4$\sqrt{2}$)2-4×4×1=16,
∴x=$\frac{4\sqrt{2}±4}{8}$=$\frac{\sqrt{2}±1}{2}$,
解得 x1=$\frac{\sqrt{2}+1}{2}$,x2=$\frac{\sqrt{2}-1}{2}$;
(2)由原方程,得
(3x+2)2-(5-2x)2=0,
(3x+2+5-2x)(3x+2-5+2x)=0,即(x+7)(5x-3)=0,
所以x+7=0或5x-3=0,
解得x1=-7,x2=$\frac{3}{5}$.
点评 本题考查了公式法和因式分解法解一元二次方程.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
8.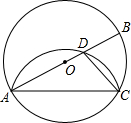 在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
 在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )| A. | 35° | B. | 40° | C. | 45° | D. | 65° |
9.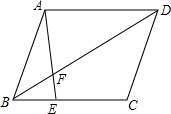 如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
 如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )| A. | 4:5 | B. | 3:5 | C. | 4:9 | D. | 3:8 |
10.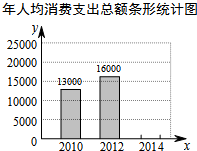 随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
年人均各项消费支出统计表
根据以上信息解答下列问题:
(1)a=5200;并补全条形统计图;
(2)我们把“食品支出总额占个人消费支出总额的百分数”叫做恩格尔系数,请分别求出小明家2010,2012,2014年的恩格尔系数,并根据变化情况谈谈你的看法.
 随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:年人均各项消费支出统计表
| 年份 支出项目(单位:元) | 2010年 | 2012年 | 2014年 |
| 食品支出 | a | 5600 | 6300 |
| 医疗、保健支出 | 2000 | 2200 | 3000 |
| 家庭用品及服务支出 | 3300 | 4000 | 5700 |
| 其他支出 | 2500 | 4200 | 6000 |
(1)a=5200;并补全条形统计图;
(2)我们把“食品支出总额占个人消费支出总额的百分数”叫做恩格尔系数,请分别求出小明家2010,2012,2014年的恩格尔系数,并根据变化情况谈谈你的看法.
 如图,设P是等边△ABC内的一点,PA=3,PB=5,PC=4,则∠APC=150°°.
如图,设P是等边△ABC内的一点,PA=3,PB=5,PC=4,则∠APC=150°°.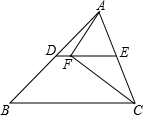 如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为60°.
如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为60°. 如图,斜坡AC的坡比为1:$\sqrt{3}$,AC=10米,坡顶有一旗杆BC,旗杆顶端B点与点A有一条彩带相连,AB=14米,试求旗杆BC的高度.
如图,斜坡AC的坡比为1:$\sqrt{3}$,AC=10米,坡顶有一旗杆BC,旗杆顶端B点与点A有一条彩带相连,AB=14米,试求旗杆BC的高度.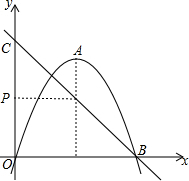 如图,抛物线y=-(x+m)2+k的顶点A的坐标为(2,4),与x轴的正半轴交于点B,点C的坐标为(0,4),点A,P关于直线BC对称.
如图,抛物线y=-(x+m)2+k的顶点A的坐标为(2,4),与x轴的正半轴交于点B,点C的坐标为(0,4),点A,P关于直线BC对称.