题目内容
15. 如图,斜坡AC的坡比为1:$\sqrt{3}$,AC=10米,坡顶有一旗杆BC,旗杆顶端B点与点A有一条彩带相连,AB=14米,试求旗杆BC的高度.
如图,斜坡AC的坡比为1:$\sqrt{3}$,AC=10米,坡顶有一旗杆BC,旗杆顶端B点与点A有一条彩带相连,AB=14米,试求旗杆BC的高度.
分析 如果延长BC交AD于E点,则CE⊥AD,要求BC的高度,就要知道BE和CE的高度,就要先求出AE的长度.直角三角形ACE中有坡比,由AC的长,那么就可求出AE的长,然后求出BE、CE的高度,BC=BE-CE,即可得出结果.
解答  解:延长BC交AD于E点,则CE⊥AD.
解:延长BC交AD于E点,则CE⊥AD.
在Rt△AEC中,AC=10,由坡比为1:$\sqrt{3}$可知:∠CAE=30°,
∴CE=AC•sin30°=10×$\frac{1}{2}$=5,
AE=AC•cos30°=5$\sqrt{3}$.
在Rt△ABE中,BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{1{4}^{2}-(5\sqrt{3})^{2}}$=11.
∵BE=BC+CE,
∴BC=BE-CE=11-5=6(米).
答:旗杆的高度为6米.
点评 考查了解直角三角形的应用,两个直角三角形有公共的直角边,先求出公共边的解决此类题目的基本出发点.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.下列调查适合普查的是( )
| A. | 调查2015年5月份市场上某品牌饮料的质量 | |
| B. | 了解中央电视台某一频道的全国收视率情况 | |
| C. | 环保部门调查2015年5月份黄河某段水域的水质量情况 | |
| D. | 了解全班同学本周末参加社区活动的时间 |
10.已知∠A=60°,则∠A的余角是( )
| A. | 160° | B. | 120° | C. | 60° | D. | 30° |
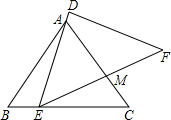 如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5,BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,BE=1或$\frac{11}{6}$.
如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5,BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,BE=1或$\frac{11}{6}$. 如图,点A、B、C在同一条直线上,AD∥BE,AD=BC,AB=BE,求证:BD=CE.
如图,点A、B、C在同一条直线上,AD∥BE,AD=BC,AB=BE,求证:BD=CE.