题目内容
18. 如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
分析 在Rt△ABO中,由∠AOB=90°、BO=5、∠BAO=30°即可求出AB、AO的长度,根据AD为⊙O的直径可得出∠ACD=90°=∠AOB,再结合∠BAO=∠DAC即可得出△ABO∽△ADC,根据相似三角形的性质即可得出$\frac{CD}{OB}=\frac{AD}{AB}$,代入数据求出CD,此题得解.
解答 解:在Rt△ABO中,∠AOB=90°,BO=5,∠BAO=30°,
∴AB=2BO=10,AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=5$\sqrt{3}$,
∴AD=2AO=10$\sqrt{3}$.
∵AD为⊙O的直径,
∴∠ACD=90°=∠AOB,
又∵∠BAO=∠DAC,
∴△ABO∽△ADC,
∴$\frac{CD}{OB}=\frac{AD}{AB}$,
∴CD=$\frac{AD•OB}{AB}$=5$\sqrt{3}$.
故选D.
点评 本题考查了相似三角形的判定与性质以及解直角三角形,根据相似三角形的性质找出$\frac{CD}{OB}=\frac{AD}{AB}$是解题的关键.

练习册系列答案
相关题目
10.下列事件发生的概率为0的是( )
| A. | 将来的某年会有370天 | B. | 小强的体重只有25公斤 | ||
| C. | 小明的爸爸买体彩中了大奖 | D. | 未来三天必有强降雨 |
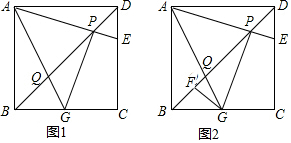
 图中,已知AB=12cm,及AC=16cm,M是BC的中点,D点及E点分别在AB和AC之上并且$\frac{AD}{AE}$=$\frac{1}{2}$,求$\frac{DX}{XE}$的值.
图中,已知AB=12cm,及AC=16cm,M是BC的中点,D点及E点分别在AB和AC之上并且$\frac{AD}{AE}$=$\frac{1}{2}$,求$\frac{DX}{XE}$的值.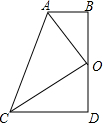 如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,AB+CD=AC.
如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,AB+CD=AC. 如图,一艘轮船在小岛A的北偏东60°方向,距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度是每小时多少海里?
如图,一艘轮船在小岛A的北偏东60°方向,距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度是每小时多少海里?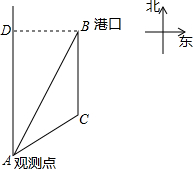 已知B港口位于A观测点北偏东30°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,30min后达到C处,现测得C处位于A观测点北偏东60°方向,则此时货轮与A观测点之间的距离AC的长是(16$\sqrt{3}$-12)km.
已知B港口位于A观测点北偏东30°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,30min后达到C处,现测得C处位于A观测点北偏东60°方向,则此时货轮与A观测点之间的距离AC的长是(16$\sqrt{3}$-12)km.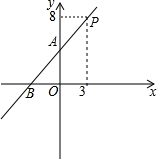 已知:如图,直线y=kx+4(k≠0)经过点P,A,B.
已知:如图,直线y=kx+4(k≠0)经过点P,A,B.