题目内容
2. 已知如图:在△ABC中,AD⊥BC于D,∠B=30°,∠C=45°,BD=2$\sqrt{3}$,求AC的长.
已知如图:在△ABC中,AD⊥BC于D,∠B=30°,∠C=45°,BD=2$\sqrt{3}$,求AC的长.
分析 先根据锐角三角函数的定义求出AD的长,再由勾股定理即可求出AC的长.
解答 解:∵AD⊥BC,
∴∠ADB=90°.
在Rt△ABD中,
∵∠B=30°,BD=2$\sqrt{3}$,
∴AD=BD•tan30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2.
在Rt△ACD中,
∵∠C=45°,
∴CD=AD=2,
∴AC=$\sqrt{{AD}^{2}+{CD}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
点评 本题考查的是解直角三角形,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
相关题目
15.一次函数y=xn+4n(n>0)的图象与x轴的交点的坐标( )
| A. | (4,0) | B. | (-4,0) | C. | (0,4) | D. | (0,-4) |
12.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表
从上表可知,下列说法(1)抛物线与x轴的一个交点为(3,0);(2)抛物线y=ax2+bx+c最大值b;(3)抛物线对称轴x=$\frac{1}{2}$;(4)在对称轴左侧y随x增大而增大,正确的个数是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.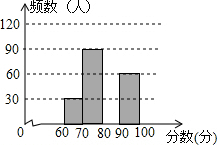 为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
(1)此次调查的样本容量为300;m=120;n=0.3;
(2)补全频数分布直方图;
(3)如果比赛成绩80分以上为优秀,那么你估计师大附中多元校区八年级学生笔试成绩的优秀人数大约是1800名.
 为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
(2)补全频数分布直方图;
(3)如果比赛成绩80分以上为优秀,那么你估计师大附中多元校区八年级学生笔试成绩的优秀人数大约是1800名.
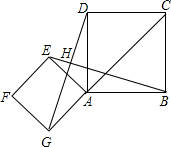 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.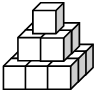 一个画家将14个边长为1m的正方形,他在地面上把它们摆成如图所示的形式,然后把露出表面的部分都涂上颜色,那么被涂上颜色的总面积的为33m2;若按此法摆放n层,那么露出表面的部分涂上颜色后的总面积可以表示为3n2+2n(m2).
一个画家将14个边长为1m的正方形,他在地面上把它们摆成如图所示的形式,然后把露出表面的部分都涂上颜色,那么被涂上颜色的总面积的为33m2;若按此法摆放n层,那么露出表面的部分涂上颜色后的总面积可以表示为3n2+2n(m2).