题目内容
7.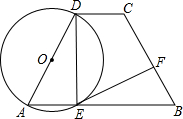 如图、在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的⊙O交AB于E,过E作
如图、在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的⊙O交AB于E,过E作EF⊥BC交BC于F.
(1)判断EF与⊙O的位置关系,并证明你的结论;
(2)若AD=5,CF=3,tan∠ADE=$\frac{3}{4}$,求CD.
分析 (1)根据已知和等腰三角形的性质可得到∠OED+∠DEF=90°,即OE⊥EF,即可证得EF是⊙O的切线;
(2)根据已知求得AE=3,利用两组角对应相等的两个三角形相似得到△ADE∽△BEF,再根据相似三角形的对应边成比例求得BE,进而即可得到CD.
解答 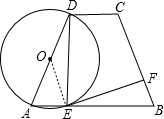 证明:(1)EF是⊙O的切线,理由如下:
证明:(1)EF是⊙O的切线,理由如下:
连接OE,
∵AD是直径,
∴∠OED+∠OEA=90°,
∵OA=OE,AD=BC,
∴∠OEA=∠A=∠B.
∴∠A=∠B=∠DEF.
∴∠OED+∠DEF=90°
∴OE⊥EF,
∴EF是⊙O的切线;
(2)∵AD=5,tan∠ADE=$\frac{3}{4}$,
∴AE=3,DE=4,
∵∠DEF+∠FEB=90°,∠A+∠ADE=90°,∠A=∠B=∠DEF.
∴∠ADE=∠FEB,
∴△ADE∽△BEF.
∴$\frac{BF}{AE}$=$\frac{BE}{AD}$.即$\frac{2}{3}$=$\frac{BE}{5}$,
∴BE=$\frac{10}{3}$,
∴CD=$\frac{10}{3}$-3=$\frac{1}{3}$.
点评 此题考查了切线的判定和性质,相似三角形的判定和性质,等腰三角形的性质,等腰梯形的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
19.双曲线y=-$\frac{2}{x}$上两点为(x1,y1)(x2,y2),且x1<x2<0,则下列说法正确的是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
12.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表
从上表可知,下列说法(1)抛物线与x轴的一个交点为(3,0);(2)抛物线y=ax2+bx+c最大值b;(3)抛物线对称轴x=$\frac{1}{2}$;(4)在对称轴左侧y随x增大而增大,正确的个数是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.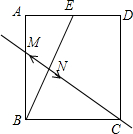 如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于$\frac{1}{2}BE$的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于$\frac{1}{2}BE$的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
 如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于$\frac{1}{2}BE$的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于$\frac{1}{2}BE$的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
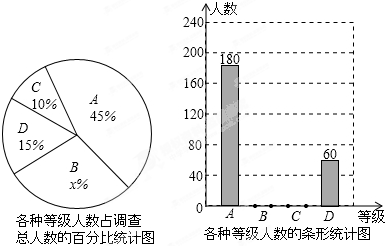
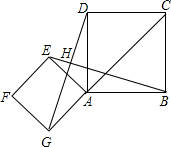 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.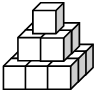 一个画家将14个边长为1m的正方形,他在地面上把它们摆成如图所示的形式,然后把露出表面的部分都涂上颜色,那么被涂上颜色的总面积的为33m2;若按此法摆放n层,那么露出表面的部分涂上颜色后的总面积可以表示为3n2+2n(m2).
一个画家将14个边长为1m的正方形,他在地面上把它们摆成如图所示的形式,然后把露出表面的部分都涂上颜色,那么被涂上颜色的总面积的为33m2;若按此法摆放n层,那么露出表面的部分涂上颜色后的总面积可以表示为3n2+2n(m2).