��Ŀ����
12��ij���еĵ��¹��ȸ��칤���ڽ���֮�����мס����������̶Ӷ��ύ��ͬһ·�ι��̵Ľ���Ͷ�귽�������̶ӵ�����Ҫ��180����ɣ��ҹ��̶ӵ�����Ҫ��120����ɣ���1������ס��������̶Ӻ�����ɴ���Ŀ����Ҫ�����죿
��2����ʩ�������У����̼�������Ҫ��һ��������Ա���ֳ��ල��ÿ�첹��200Ԫ�����ɼ��̶ӵ���ʩ����ƽ��ÿ����֧�������̶ӵķ���Ϊ2��Ԫ��Ϊ�����̹��ڣ�����Ŀ�������ɼס����������̶Ӻ�����ɣ���Ҫ�������ɸ���Ŀ���ܷ�������̶ӵ�����ɸ���Ŀ���ܷ�����ͬ����ƽ��ÿ����֧�����ҹ��̶ӵķ���Ϊ������Ԫ��
��ע��ʩ������Ŀ���ܷ���=֧�������̶ӵ��ܷ���+֧����������Ա�������ܷ��ã�
���� ��1����ס��������̶Ӻ�����ɴ���Ŀ����Ҫx�죬�������⽨�����������⼴�ɣ�
��2�����ҹ��̶�ƽ��ÿ���ʩ������Ϊa��Ԫ����Ҫ�������ɸ���Ŀ���ܷ�������̶ӵ�����ɸ���Ŀ���ܷ�����ͬ�������������⼴�ɣ�
��� �⣺��1����ס��������̶Ӻ�����ɴ���Ŀ����Ҫx�죬�ɵã�$\frac{1}{120}x+\frac{1}{180}x=1$��
��ã�x=72��
�𣺼ס��������̶Ӻ�����ɴ���Ŀ����Ҫ72�죻
��2�����ҹ��̶�ƽ��ÿ���ʩ������ΪaԪ�������⣬��
72a+72��20000+200��72=200��180+200��180
a=1200
���ҹ��̶�ƽ��ÿ���ʩ���������1.2��Ԫ��
���� ���⿼���˹��������������ϵ������Ч�ʡ�����ʱ��=�������������ã���һԪһ�β���ʽ����ʵ����������ã���ʽ���̵Ľⷨ�����ã����ʱ���ݼס������Ӻ�����ɸ���Ŀ����72�콨����������ס��ҵ��������Ҫ��ʱ���ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
17�� ��ͼ��E��F��G��H�ֱ���BD��BC��AC��AD���е㣬��AB=CD�����н��ۣ���EG�AFH�� ���ı���EFGH�Ǿ��Σ���HFƽ�֡�EHG�����ı���EFGH�����Σ�������ȷ�Ľ����У�����������
��ͼ��E��F��G��H�ֱ���BD��BC��AC��AD���е㣬��AB=CD�����н��ۣ���EG�AFH�� ���ı���EFGH�Ǿ��Σ���HFƽ�֡�EHG�����ı���EFGH�����Σ�������ȷ�Ľ����У�����������
 ��ͼ��E��F��G��H�ֱ���BD��BC��AC��AD���е㣬��AB=CD�����н��ۣ���EG�AFH�� ���ı���EFGH�Ǿ��Σ���HFƽ�֡�EHG�����ı���EFGH�����Σ�������ȷ�Ľ����У�����������
��ͼ��E��F��G��H�ֱ���BD��BC��AC��AD���е㣬��AB=CD�����н��ۣ���EG�AFH�� ���ı���EFGH�Ǿ��Σ���HFƽ�֡�EHG�����ı���EFGH�����Σ�������ȷ�Ľ����У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
1��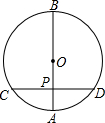 ��ͼ���ڡ�O�У�ֱ��AB��ֱ����CD������ΪP����PA=4��PB=12����CP�ij�Ϊ��������
��ͼ���ڡ�O�У�ֱ��AB��ֱ����CD������ΪP����PA=4��PB=12����CP�ij�Ϊ��������
 ��ͼ���ڡ�O�У�ֱ��AB��ֱ����CD������ΪP����PA=4��PB=12����CP�ij�Ϊ��������
��ͼ���ڡ�O�У�ֱ��AB��ֱ����CD������ΪP����PA=4��PB=12����CP�ij�Ϊ��������| A�� | 2$\sqrt{3}$ | B�� | 4 | C�� | 8 | D�� | 4$\sqrt{3}$ |
2��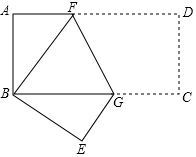 ��ͼ���ھ���ABCD�У�AB=2��BC=4���Ѿ����۵���ʹ��D���B�غϣ���C���ڵ�E�������ۺ�FG�ij�Ϊ��������
��ͼ���ھ���ABCD�У�AB=2��BC=4���Ѿ����۵���ʹ��D���B�غϣ���C���ڵ�E�������ۺ�FG�ij�Ϊ��������
 ��ͼ���ھ���ABCD�У�AB=2��BC=4���Ѿ����۵���ʹ��D���B�غϣ���C���ڵ�E�������ۺ�FG�ij�Ϊ��������
��ͼ���ھ���ABCD�У�AB=2��BC=4���Ѿ����۵���ʹ��D���B�غϣ���C���ڵ�E�������ۺ�FG�ij�Ϊ��������| A�� | 2.5 | B�� | 3 | C�� | $\sqrt{5}$ | D�� | 2$\sqrt{5}$ |
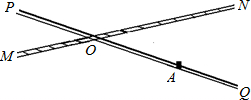 ��ͼ����·MN��·PQ�ڵ�O�����㣬��QON=30�㣬�ڵ�A����һ������¥��AO=200m���������ʻʱ����Χ200m���ڻ��ܵ�������Ӱ�죬��ô������·MN����ON������ʻʱ������¥�Ƿ���ܵ�������Ӱ�죿�������ʻ���ٶ�Ϊ72km/h������¥������Ӱ���ʱ��ԼΪ�����루��ȷ��0.1s����
��ͼ����·MN��·PQ�ڵ�O�����㣬��QON=30�㣬�ڵ�A����һ������¥��AO=200m���������ʻʱ����Χ200m���ڻ��ܵ�������Ӱ�죬��ô������·MN����ON������ʻʱ������¥�Ƿ���ܵ�������Ӱ�죿�������ʻ���ٶ�Ϊ72km/h������¥������Ӱ���ʱ��ԼΪ�����루��ȷ��0.1s����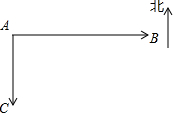 ��ͼ���״���15ǧ��/Сʱ���ٶȴӸۿ�A�����Ϸ����У�ͬʱ�Ҵ���20ǧ��/Сʱ���ٶȴӸۿ�B��ۿ�A�����У���֪�ۿ�B�ڸۿ�A���������������80ǧ�ף�����ʻ2Сʱ���������50ǧ�ף�
��ͼ���״���15ǧ��/Сʱ���ٶȴӸۿ�A�����Ϸ����У�ͬʱ�Ҵ���20ǧ��/Сʱ���ٶȴӸۿ�B��ۿ�A�����У���֪�ۿ�B�ڸۿ�A���������������80ǧ�ף�����ʻ2Сʱ���������50ǧ�ף�