题目内容
2.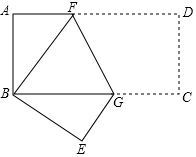 如图,在矩形ABCD中,AB=2,BC=4,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为( )
如图,在矩形ABCD中,AB=2,BC=4,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为( )| A. | 2.5 | B. | 3 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
分析 先连接BD,在Rt△ABD中,求得BD的长,在Rt△ABE中运用勾股定理求得BF的长,即可得到DF长,最后在Rt△DOF中求得FO的长,即可得到FG的长.
解答 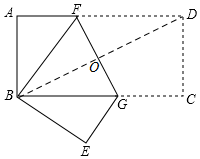 解:如图,连接BD,交EF于O,则由轴对称的性质可知,FG垂直平分BD,
解:如图,连接BD,交EF于O,则由轴对称的性质可知,FG垂直平分BD,
Rt△ABD中,BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=2$\sqrt{5}$
∴DO=$\sqrt{5}$,
由折叠可得,∠BFO=∠DFO,
由AD∥BC可得,∠DFO=∠BGO,
∴∠BFO=∠BGO,
∴BF=BG,即△BFG是等腰三角形,
∴BD平分FG,
设BF=DF=x,则AE=4-x,
在Rt△ABE中,(4-x)2+22=x2,
解得x=$\frac{5}{2}$,即DF=$\frac{5}{2}$,
∴Rt△DOF中,OF=$\sqrt{D{F}^{2}-D{O}^{2}}$=$\frac{\sqrt{5}}{2}$,
∴FG=2FO=$\sqrt{5}$.
故选:C.
点评 本题是折叠问题,主要考查了折叠的性质,勾股定理以及矩形的性质的综合应用,解决问题的关键是根据勾股定理列方程求解.本题也可以运用面积法求得FO的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.在平面直角坐标系中,函数y=-x+1的图象经过( )
| A. | 第一,二,三象眼 | B. | 第二,三,四象限 | C. | 第一,二,四象限 | D. | 第一,三,四象限 |
10.已知$\frac{c}{4}$=$\frac{b}{5}$=$\frac{a}{6}$≠0,则$\frac{b+c}{a}$的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
17.若a>1,则a,-a,$\frac{1}{a}$从大到小排列正确的是( )
| A. | a>-a>$\frac{1}{a}$ | B. | a>$\frac{1}{a}$>-a | C. | $\frac{1}{a}$>-a>a | D. | $\frac{1}{a}$>-a>a> |
7.甲队有工人96人,乙队有工人72人,如果要求乙队的人数是甲队人数的$\frac{1}{3}$,应从乙队调 多少人去甲队?如果设应从乙队调x人到甲队,列出的方程正确的是( )
| A. | 96+x=$\frac{1}{3}$(72-x) | B. | $\frac{1}{3}$(96+x)=72-x | C. | $\frac{1}{3}$(96-x)=72-x | D. | $\frac{1}{3}$×96+x=72-x |
14.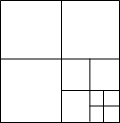 如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
 如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )| A. | ($\frac{1}{4}$)5 | B. | ($\frac{1}{2}$)5 | C. | $\frac{1}{5}$ | D. | 1-($\frac{1}{4}$)5 |
11.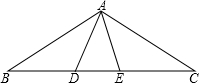 如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
 如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )| A. | 20° | B. | 50° | C. | 30° | D. | 40° |