题目内容
1．
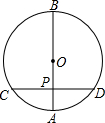如图，在⊙O中，直径AB垂直于弦CD，垂足为P，若PA=4，PB=12，则CP的长为（ ）| A． | 2$\sqrt{3}$ | B． | 4 | C． | 8 | D． | 4$\sqrt{3}$ |
分析 根据垂径定理得到CP=PD，根据相交弦定理计算即可．
解答 解：∵直径AB垂直于弦CD，
∴CP=PD，
由相交弦定理得，CP•PD=PA•PB=4×12=48，
解得，CP=4$\sqrt{3}$，
故选：D．
点评 本题考查的是垂径定理的应用，掌握垂直弦的直径平分这条弦，并且平分弦所对的两条弧是解题的关键．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
11．
如图所示，△ABC的两条外角平分线AP、CP相交于点P，PH⊥AC于H．若∠ABC=60°，则下面的结论：
①∠ABP=30°；②∠APC=60°；③PB=2PH；④∠APH=∠BPC，
其中正确结论的个数是（ ）
如图所示，△ABC的两条外角平分线AP、CP相交于点P，PH⊥AC于H．若∠ABC=60°，则下面的结论：①∠ABP=30°；②∠APC=60°；③PB=2PH；④∠APH=∠BPC，
其中正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
9．
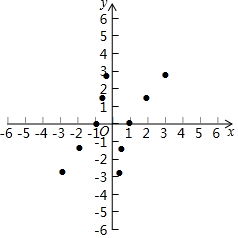有这样一个问题：探究函数y=$\frac{{x}^{2}-1}{x}$的图象与性质：
小宏根据学习函数的经验，对函数y=$\frac{{x}^{2}-1}{x}$的图象与性质进行了探究．
下面是小宏的探究过程，请补充完整：
（1）函数y=$\frac{{x}^{2}-1}{x}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值
求m，n的值；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对应值为坐标的点，根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的性质（两条即可）：①x＜0时，函数y随x的增大而增大．②x＞0时，函数y随x的增大而增大．．
有这样一个问题：探究函数y=$\frac{{x}^{2}-1}{x}$的图象与性质：小宏根据学习函数的经验，对函数y=$\frac{{x}^{2}-1}{x}$的图象与性质进行了探究．
下面是小宏的探究过程，请补充完整：
（1）函数y=$\frac{{x}^{2}-1}{x}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{8}{3}$ | -$\frac{3}{2}$ | 0 | m | $\frac{8}{3}$ | -$\frac{8}{3}$ | -$\frac{3}{2}$ | 0 | $\frac{3}{2}$ | n | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对应值为坐标的点，根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的性质（两条即可）：①x＜0时，函数y随x的增大而增大．②x＞0时，函数y随x的增大而增大．．
16．关于x的一元二次方程x2+4x-2k=0有两个实数根，则实数k的取值范围是（ ）
| A． | k≥-2 | B． | k≤-2 | C． | k＞-2 | D． | k=-2 |
13．在平面直角坐标系中，函数y=-x+1的图象经过（ ）
| A． | 第一，二，三象眼 | B． | 第二，三，四象限 | C． | 第一，二，四象限 | D． | 第一，三，四象限 |
10．已知$\frac{c}{4}$=$\frac{b}{5}$=$\frac{a}{6}$≠0，则$\frac{b+c}{a}$的值为（ ）
| A． | 1 | B． | $\frac{3}{2}$ | C． | 2 | D． | 4 |
11．
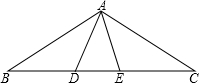如图，∠ADB=∠AEC=100°，∠BAD=50°，BD=EC，则∠C=（ ）
如图，∠ADB=∠AEC=100°，∠BAD=50°，BD=EC，则∠C=（ ）| A． | 20° | B． | 50° | C． | 30° | D． | 40° |