题目内容
17. 已知直线y=2x+7与直线y=-2x-3相交于点C.
已知直线y=2x+7与直线y=-2x-3相交于点C.(1)求两条直线的交点C的坐标;
(2)求△ABC的面积;
(3)结合图象回答:当x取何值时,2x+7>-2x-3?当x取何值时,2x+7<-2x-3?
分析 (1)根据两条直线相交的问题,通过解方程组$\left\{\begin{array}{l}{y=2x+7}\\{y=-2x-3}\end{array}\right.$得到C点坐标;
(2)根据三角形面积公式计算;
(3)观察函数图象得,当x>-$\frac{5}{2}$时,直线2x+7在直线y=-2x-3的上方;当x<-$\frac{5}{2}$时,2x+7<-2x-3.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=2x+7}\\{y=-2x-3}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{5}{2}}\\{y=2}\end{array}\right.$,
所以C点坐标为(-$\frac{5}{2}$,2);
(2)当x=0时,y=2x+7=7,则A(0,7);当x=0时,y=-2x-3=-3,则B(0,-3),
所以S△ABC=$\frac{1}{2}$×(7+3)×$\frac{5}{2}$=$\frac{25}{2}$;
(3)当x>-$\frac{5}{2}$时,2x+7>-2x-3;当x<-$\frac{5}{2}$时,2x+7<-2x-3.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
8. 如图,正方形ABCD中,点E是AD边中点,BD、CE交于点H,BE、AH交于点G,则下列结论:
如图,正方形ABCD中,点E是AD边中点,BD、CE交于点H,BE、AH交于点G,则下列结论:
①AG⊥BE;②BG=4GE;③S△BHE=S△CHD;④∠AHB=∠EHD.
其中正确的个数是( )
 如图,正方形ABCD中,点E是AD边中点,BD、CE交于点H,BE、AH交于点G,则下列结论:
如图,正方形ABCD中,点E是AD边中点,BD、CE交于点H,BE、AH交于点G,则下列结论:①AG⊥BE;②BG=4GE;③S△BHE=S△CHD;④∠AHB=∠EHD.
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4. 如图所示,某计算装置有一数据入口A和一运算结果出口B,下表给出的是小红输入的数字及所得的运算结果
如图所示,某计算装置有一数据入口A和一运算结果出口B,下表给出的是小红输入的数字及所得的运算结果
若小红输入的数为49,输出的结果应为多少?若小红输入的数字为a,你能用a表示输出结果吗?
 如图所示,某计算装置有一数据入口A和一运算结果出口B,下表给出的是小红输入的数字及所得的运算结果
如图所示,某计算装置有一数据入口A和一运算结果出口B,下表给出的是小红输入的数字及所得的运算结果| A | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| B | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
5. 如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )
如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )
 如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )
如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,AB∥DE,点F、C在AD上,AB=DE,且AF=FC=CD.
如图,AB∥DE,点F、C在AD上,AB=DE,且AF=FC=CD.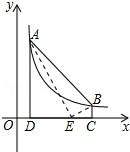 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.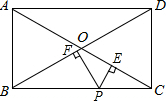 已知矩形ABCD对角线AC,BD交于点O,点P为BC边上任意一点,PE⊥AC于点E,PF⊥BD于点F,∠AOD=120°,AC=8,求PE+PF的值.
已知矩形ABCD对角线AC,BD交于点O,点P为BC边上任意一点,PE⊥AC于点E,PF⊥BD于点F,∠AOD=120°,AC=8,求PE+PF的值.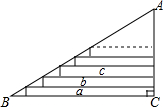 如图,在△ABC中,已知∠C=90°,AC=60,AB=100,a,b,c…是在△ABC内部的矩形,它们的一个顶点在AB上,一组对边分别在AC上或与AC平行,另一组对边分别在BC上或与BC平行.若各矩形在AC上的边长相等,矩形a的一边长是72,则这样的矩形a、b、c…的个数是( )
如图,在△ABC中,已知∠C=90°,AC=60,AB=100,a,b,c…是在△ABC内部的矩形,它们的一个顶点在AB上,一组对边分别在AC上或与AC平行,另一组对边分别在BC上或与BC平行.若各矩形在AC上的边长相等,矩形a的一边长是72,则这样的矩形a、b、c…的个数是( )