题目内容
2.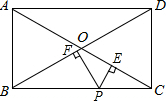 已知矩形ABCD对角线AC,BD交于点O,点P为BC边上任意一点,PE⊥AC于点E,PF⊥BD于点F,∠AOD=120°,AC=8,求PE+PF的值.
已知矩形ABCD对角线AC,BD交于点O,点P为BC边上任意一点,PE⊥AC于点E,PF⊥BD于点F,∠AOD=120°,AC=8,求PE+PF的值.
分析 先证明△AOB是等边三角形,得出AB=OA=OB=4,由勾股定理求出BC,由△OBC面积=△OBP的面积+△COP的面积=$\frac{1}{4}$矩形ABCD的面积,即可得出结果.
解答 解:连接OP,如图所示:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC=$\frac{1}{2}$AC=4,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,△OBC面积=$\frac{1}{4}$矩形ABCD的面积,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB时等边三角形,
∴AB=OA=OB=4,
∴BC=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∵△OBC的面积=△OBP的面积+△COP的面积
=$\frac{1}{2}$OB•PF+$\frac{1}{2}$OC•PE=$\frac{1}{2}$OB(PE+PF)=$\frac{1}{4}$AB×BC,
即$\frac{1}{2}$×4×(PE+PF)=$\frac{1}{4}$×4×4$\sqrt{3}$,
∴PE+PF=2$\sqrt{3}$.
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理、三角形面积和矩形面积的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
10.定义运算:a?b=a(1-b).下面给出了关于这种运算的几种结论:①2?(-2)=6,②a?b=b?a,③若a+b=0,则(a?a)+(b?b)=2ab,④若a?b=0,则a=0或b=1,其中结论正确的序号是( )
| A. | ①④ | B. | ①③ | C. | ②③④ | D. | ①③④ |
12. 如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
 如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )| A. | $\frac{3}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
9.下列哪种情况下,直线a与b不一定是平行线( )
| A. | a与b是不相交的两条直线 | B. | a与b被直线c所截,且内错角互补 | ||
| C. | a与b都平行于直线c | D. | a与b被直线c所截,且同位角相等 |
 在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2次碰到矩形的边时,点P的坐标为(7,4);当点P第6次碰到矩形的边时,点P的坐标为(0,3);当点P第2015次碰到矩形的边时,点P的坐标为(1,4).
在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2次碰到矩形的边时,点P的坐标为(7,4);当点P第6次碰到矩形的边时,点P的坐标为(0,3);当点P第2015次碰到矩形的边时,点P的坐标为(1,4).
 已知直线y=2x+7与直线y=-2x-3相交于点C.
已知直线y=2x+7与直线y=-2x-3相交于点C. 如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C的位置,使B在斜边A′B′上,A′C与AB相交于D,∠BDC的度数为90°.
如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C的位置,使B在斜边A′B′上,A′C与AB相交于D,∠BDC的度数为90°.