Question

12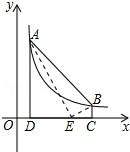．如图，点A（m，6）、B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．
（1）求m、n的值并写出该反比例函数的解析式．
（2）点E在线段CD上，S_△ABE=10，求点E的坐标．

Answer 1

分析 （1）根据题意列出关于m与n的方程组，求出方程组的解得到m与n的值，确定出A与B坐标，设出反比例函数解析式，将A坐标代入即可确定出解析式；
（2）设E（x，0），表示出DE与CE，连接AE，BE，三角形ABE面积=四边形ABCD面积-三角形ADE面积-三角形BCE面积，求出即可．

解答 解：（1）由题意得：$\left\{\begin{array}{l}{6m=n}\\{m+5=n}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=1}\\{n=6}\end{array}\right.$，
∴A（1，6），B（6，1），
设反比例函数解析式为y=$\frac{k}{x}$，
将A（1，6）代入得：k=6，
则反比例解析式为y=$\frac{6}{x}$；
（2）设E（x，0），则DE=x-1，CE=6-x，
∵AD⊥x轴，BC⊥x轴，
∴∠ADE=∠BCE=90°，
连接AE，BE，
则S_△ABE=S_{四边形ABCD}-S_△ADE-S_△BCE
=$\frac{1}{2}$（BC+AD）•DC-$\frac{1}{2}$DE•AD-$\frac{1}{2}$CE•BC
=$\frac{1}{2}$×（1+6）×5-$\frac{1}{2}$（x-1）×6-$\frac{1}{2}$（6-x）×1
=$\frac{35}{2}$-$\frac{5}{2}$x
=10，
解得：x=3，
则E（3，0）．

点评 此题考查了待定系数法求反比例函数解析式，反比例函数图象上点的坐标特征，熟练掌握待定系数法是解本题的关键．