题目内容
5.一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的距离y1(km)与行驶的时间x(h)之间的函数关系如图1中线段AB所示;慢车离乙地的距离y2(km)与行驶的时间x (h)之间的函数关系如图1中线段OC所示.根据图象进行以下研究.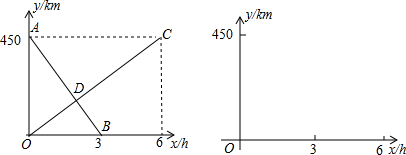
(1)分别求线段AB、OC对应的函数解析式y1、y2;
(2)设快、慢车之间的距离为S,求S(km)与慢车行驶时间x(h)的函数关系式,并画出函数的图象;
(3)求快、慢车之间的距离超过135km时,x的取值范围.
分析 (1)利用点A坐标为(0,450),可以得出甲,乙两地之间的距离为450,利用点A坐标为(0,450),点B坐标为(3,0),代入y1=kx+b求出即可,利用线段OC解析式为y=ax求出即可;
(2)利用(1)中所求得出S=|y1-y2|,进而求出函数解析式,得出图象即可.
(3)S=135时,分两种情况:-225x+450=135或225x-450=135,解得:x=1.4或x=2.6则快、慢车之间的距离超过135km时,x的取值范围:0≤x<1.4或2.6<x≤6.
解答 解:(1)设线段AB的函数解析式为y1=kx+b,
把点A坐标为(0,450),点B坐标为(3,0),代入y1=kx+b得:$\left\{\begin{array}{l}{b=450}\\{3k+b=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-150}\\{b=450}\end{array}\right.$
则y1=-150x+450,
设线段OC的函数解析式为y=ax,
把(6,450)代入y=ax得:6a=450,
解得:a=75,
则y2=75x.
(2)根据(1)得出,
S=|y1-y2|=|450-150x--75x|=$\left\{\begin{array}{l}{-225x+450(0≤x≤2)}\\{225x-450(2<x≤3)}\\{75x(3<x≤6)}\end{array}\right.$
函数图象如图所示:
(3)S=135时,分两种情况:
-225x+450=135或225x-450=135,
解得:x=1.4或x=2.6
则快、慢车之间的距离超过135km时,x的取值范围:0≤x<1.4或2.6<x≤6.
点评 此题主要考查了一次函数的应用和待定系数法求解析式,根据已知图象上的点得出函数解析式以及利用分段函数分析是解题关键.

 如图,从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )
如图,从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
 如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数
如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数 ,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.
,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.
 如图,一艘轮船在A处发现有一灯塔C在正北方向上,它沿北偏东30°方向以20海里/时的速度航行1小时后到达B处,发现灯塔C在正西方向上,则此时轮船与灯塔C的距离为20海里.
如图,一艘轮船在A处发现有一灯塔C在正北方向上,它沿北偏东30°方向以20海里/时的速度航行1小时后到达B处,发现灯塔C在正西方向上,则此时轮船与灯塔C的距离为20海里.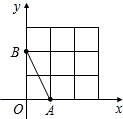 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上. 某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度.
某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度.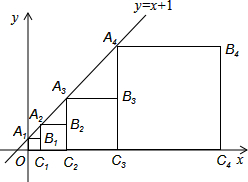 如图,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;…依此类推,则第n个正方形的边长为( )
如图,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;…依此类推,则第n个正方形的边长为( ) 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=4,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,则AD的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=4,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,则AD的长为( )