题目内容
20.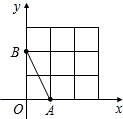 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.(1)求线段AB所在直线的函数解析式;
(2)将线段AB绕点B逆时针旋转90°,得到线段BC,指定位置画出线段BC.若直线BC的函数解析式为y=kx+b,则y随x的增大而增大(填“增大”或“减小”).
分析 (1)设直线AB解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可确定出直线AB解析式;
(2)如图所示,做出线段BC,利用待定系数法确定出直线BC解析式,即可做出判断.
解答 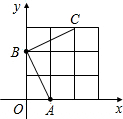 解:(1)根据题意得:A(1,0),B(0,2),
解:(1)根据题意得:A(1,0),B(0,2),
设线段AB所在的直线解析式为y=kx+b,
把A与B坐标代入得:$\left\{\begin{array}{l}{k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
则线段AB所求直线解析式为y=-2x+2;
(2)如图所示,B(0,2),C(2,3),
设直线BC解析式为y=kx+b,
把B与C坐标代入得:$\left\{\begin{array}{l}{b=2}\\{2k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,即直线BC解析式为y=$\frac{1}{2}$x+2,
则y随x的增大而增大,
故答案为:(2)增大
点评 此题考查了待定系数法求一次函数解析式,以及一次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
8.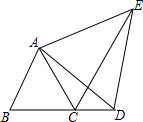 如图,等边△ABC,点D在BC的延长线上,连接AD,以AD为边作等边△ADE,连接CE
如图,等边△ABC,点D在BC的延长线上,连接AD,以AD为边作等边△ADE,连接CE
(1)求证:BD=CE;
(2)当点D在BC的延长线上移动时,∠ECD的度数不会发生变化,请你对此结论进行证明.
 如图,等边△ABC,点D在BC的延长线上,连接AD,以AD为边作等边△ADE,连接CE
如图,等边△ABC,点D在BC的延长线上,连接AD,以AD为边作等边△ADE,连接CE(1)求证:BD=CE;
(2)当点D在BC的延长线上移动时,∠ECD的度数不会发生变化,请你对此结论进行证明.
12. 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形DBCE的面积比为( )
如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形DBCE的面积比为( )
 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形DBCE的面积比为( )
如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形DBCE的面积比为( )| A. | 1:2 | B. | 1:4 | C. | 1:3 | D. | 4:1 |
10.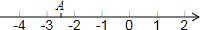 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )
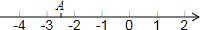 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )| A. | -$\sqrt{2}$ | B. | -$\sqrt{8}$ | C. | -$\sqrt{5}$ | D. | -$\sqrt{10}$ |
 (1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点,求线段MN的长度;
(1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点,求线段MN的长度;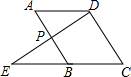 如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于E点,求证:BE=AD.
如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于E点,求证:BE=AD. 如图,M是弦AB(非直径)的中点,弦CD与弦AB相交于点M.当DC是⊙O直径时,CD⊥AB(只需填一个符合要求的答案).
如图,M是弦AB(非直径)的中点,弦CD与弦AB相交于点M.当DC是⊙O直径时,CD⊥AB(只需填一个符合要求的答案).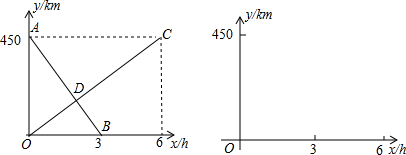
 已知a、b、c在数轴上的位置如图所示,试求|a+b|-|c-3|+|b-c|的值.
已知a、b、c在数轴上的位置如图所示,试求|a+b|-|c-3|+|b-c|的值.