题目内容
14．
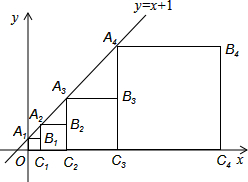如图，直线y=x+1与y轴相交于点A1，以OA1为边作正方形OA1B1C1，记作第一个正方形；延长C1B1与直线y=x+1相交于点A2，再以C1A2为边作正方形C1A2B2C2，记作第二个正方形；…依此类推，则第n个正方形的边长为（ ）| A． | 2n | B． | 2n-1 | C． | 2n | D． | 2n+1 |
分析 解题的关键是求出第一个正方体的边长，然后依次计算n=1，n=2…总结出规律．
解答 解：根据题意不难得出第一个正方体的边长=1，
那么：n=1时，第1个正方形的边长为：1=20
n=2时，第2个正方形的边长为：2=21
n=3时，第3个正方形的边长为：4=22
…
第n个正方形的边长为：2n-1．
故选B．
点评 本题考查的是一次函数图象上点的坐标特点，解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论．
练习册系列答案
相关题目
4．
如图，将△ABC绕点C按逆时针方向旋转到△A′B′C′的位置，若∠BCB′=30°，则∠ACA′的大小为（ ）
如图，将△ABC绕点C按逆时针方向旋转到△A′B′C′的位置，若∠BCB′=30°，则∠ACA′的大小为（ ）| A． | 20° | B． | 30° | C． | 35° | D． | 40° |
已知a、b、c在数轴上的位置如图所示，试求|a+b|-|c-3|+|b-c|的值．
19．若（m-1）x＞m-1的解集为x＜1，则m的取值范围是（ ）
| A． | m＞1 | B． | m＜1 | C． | m＞0 | D． | m＜0 |
6．
如图，△ABC中，∠C=90°，∠A=30°，BD平分∠ABC，则∠BDC的度数为（ ）
如图，△ABC中，∠C=90°，∠A=30°，BD平分∠ABC，则∠BDC的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
3．
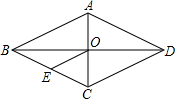已知：如图，菱形ABCD对角线AC与BD相交于点O，E为BC的中点E，AD=6cm，则OE的长为（ ）
已知：如图，菱形ABCD对角线AC与BD相交于点O，E为BC的中点E，AD=6cm，则OE的长为（ ）| A． | 6cm | B． | 4cm | C． | 3cm | D． | 2cm |
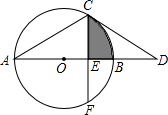如图，AB为⊙O的直径，点C在⊙O上，过点C作CD交AB的延长线于点D，已知∠D=30°，弦CF⊥AB，垂足为E，且AC=2CE．