题目内容
5.如图,下列图形都是由面积为1的正方形按一定的规律拼成,其中第1个图形是由面积为1的两个正方形拼成,第2个图形是由面积为1的五个正方形图形拼成,第3个图形是由面积为1的九个正方形拼成,…,按此规律拼图,并解答下两问:
(1)填表:
| 图形标号 | ① | ② | ③ | ④ | … | ⑥ | … |
| 小正方形的个数 | 2 | 5 | 9 | 14 | … | 27 | … |
分析 (1)第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,得第(6)个图形中面积为1的正方形的个数为2+3+4+5+6+7;
(2)由(1)中规律可得,第n个图形中面积为1的正方形有2+3+4+…+(n+1)个.
解答 解:(1)∵第(1)个图形中面积为1的正方形有2个,
第(2)个图形中面积为1的图象有2+3=5个,
第(3)个图形中面积为1的正方形有2+3+4=9个,
…,
∴第(6)个图形中面积为1的正方形的个数为2+3+4+5+6+7=27个
(2)由(1)中规律可知,第n个图形中面积为1的正方形有2+3+4+…+(n+1)=$\frac{n(n+3)}{2}$个;
故答案为:(1)27.
点评 此题考查图形的变化规律,找出图形与数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
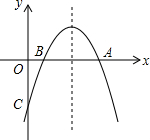 如图,抛物线y=ax2+bx+c经过A(8,0),B(2,0),C(0,-6)三点.
如图,抛物线y=ax2+bx+c经过A(8,0),B(2,0),C(0,-6)三点.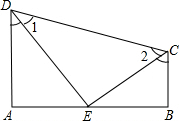 如图:已知DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°
如图:已知DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90° 如图所示是用棋子摆成的“小雨伞”:摆第一个“小雨伞”用了9个棋子,摆第二个“小雨伞”用了12个棋子,摆第三个“小雨伞”用了15个棋子,…依次规律,用75个棋子摆成的“小雨伞”是第几个图形( )
如图所示是用棋子摆成的“小雨伞”:摆第一个“小雨伞”用了9个棋子,摆第二个“小雨伞”用了12个棋子,摆第三个“小雨伞”用了15个棋子,…依次规律,用75个棋子摆成的“小雨伞”是第几个图形( )