题目内容
2.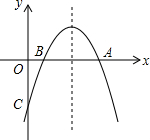 如图,抛物线y=ax2+bx+c经过A(8,0),B(2,0),C(0,-6)三点.
如图,抛物线y=ax2+bx+c经过A(8,0),B(2,0),C(0,-6)三点.(1)求抛物线的解析式;
(2)如图,在抛物线的对称轴上是否存在点P,使得四边形PB0C的周长最小?若存在,求出四边形PB0C周长的最小值;若不存在,请说明理由.
分析 (1)设交点式为y=a(x-8)(x-2),然后把C点坐标代入求出a=-$\frac{3}{8}$,于是得到抛物线解析式为y=-$\frac{3}{8}$x2+$\frac{15}{4}$x-6;
(2)先确定抛物线的对称轴为直线x=5,连结BC交直线x=5于点P,如图,利用对称性得到PA=PB,所以PB+PC=PC+PA=AC,根据两点之间线段最短得到PC+PB最短,于是可判断此时四边形PBOC的周长最小,然后计算出AC=10,再计算OC+OB+AC即可.
解答 解:(1)设抛物线解析式为y=a(x-8)(x-2),
把C(0,-6)代入得a•(-8)•(-2)=-6,解得a=-$\frac{3}{8}$,
所以抛物线解析式为y=-$\frac{3}{8}$(x-8)(x-2),即y=-$\frac{3}{8}$x2+$\frac{15}{4}$x-6;
(2)存在.
因为A(8,0),B(2,0),
所以抛物线的对称轴为直线x=5,
连结AC交直线x=5于点P,如图,则PA=PB,PB+PC=PC+PA=AC,此时PC+PB最短,
所以此时四边形PBOC的周长最小,
因为AC=$\sqrt{{8}^{2}+{6}^{2}}$=10,
所以四边形PBOC周长的最小值为2+6+10=18.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了最短路径问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.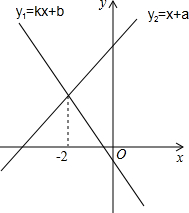 一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
 一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )| A. | x>-2 | B. | x<-2 | C. | x≤-2 | D. | x≥-2 |
5.如图,下列图形都是由面积为1的正方形按一定的规律拼成,其中第1个图形是由面积为1的两个正方形拼成,第2个图形是由面积为1的五个正方形图形拼成,第3个图形是由面积为1的九个正方形拼成,…,按此规律拼图,并解答下两问:

(1)填表:
(2)当图形标号为n时,请问第n个图形中需要多少个小正方形?

(1)填表:
| 图形标号 | ① | ② | ③ | ④ | … | ⑥ | … |
| 小正方形的个数 | 2 | 5 | 9 | 14 | … | 27 | … |
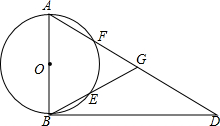 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点F,E,点D在AC的延长线上,且∠CBD=$\frac{1}{2}$∠CAB.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点F,E,点D在AC的延长线上,且∠CBD=$\frac{1}{2}$∠CAB.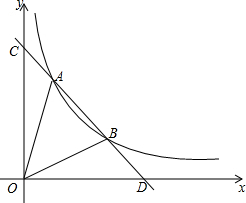 如图,一次函数的图形与y轴、x轴交于C、D两点,与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A、B两点,且AB=2BD,则△AOB的面积为8.
如图,一次函数的图形与y轴、x轴交于C、D两点,与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A、B两点,且AB=2BD,则△AOB的面积为8.