题目内容
4.某校乒乓球队有水平相当的A,B,C,D四名队员.(1)若将A,B,C,D四名队员随机平均分成甲、乙两组进行乒乓球单打练习,求A、B恰好分在一组的概率.
(2)若从A,B,C,D四名队员中随机抽取两名代表学较参加比赛,求A、B恰好披抽中的概率.
分析 (1)列举出所有情况,看A、B被分在同一组的情况数占总情况数的多少即可;
(2)画出树状图,然后由树状图求得所有等可能的结果与甲、乙两名选手恰好被抽到的情况,再利用概率公式求解即可求得答案.
解答 解:(1)所有可能出现的结果如下
| 甲组 | 乙组 | 结果 |
| AB | CD | (AB,CD) |
| AC | BD | (AC,BD) |
| AD | BC | (AD,BC) |
| BC | AD | (BC,AD) |
| BD | AC | (BD,AC) |
| CD | AB | (CD,AB) |
所有结果中,满足AB在同一组的结果有2种,
∴AB恰好分在同一组的概率=$\frac{2}{6}$=$\frac{1}{3}$;
(2)画树状图如下:

共有12种等可能的结果,甲、乙两名选手恰好被抽中的有2种情况,
∴甲、乙两名选手恰好被抽中的概率=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
9.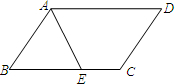 如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
 如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )
如图,?ABCD的周长为16,∠BAD的平分线AE交CD于点E,若BE=2,则CE等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.在下列手机软件图标中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.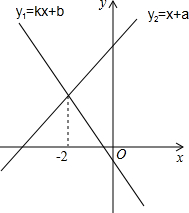 一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
 一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )
一次函数y1=kx+b与y2=x+a的图象如图,则关于x的不等式kx+b>x+a的解集是( )| A. | x>-2 | B. | x<-2 | C. | x≤-2 | D. | x≥-2 |
5.如图,下列图形都是由面积为1的正方形按一定的规律拼成,其中第1个图形是由面积为1的两个正方形拼成,第2个图形是由面积为1的五个正方形图形拼成,第3个图形是由面积为1的九个正方形拼成,…,按此规律拼图,并解答下两问:

(1)填表:
(2)当图形标号为n时,请问第n个图形中需要多少个小正方形?

(1)填表:
| 图形标号 | ① | ② | ③ | ④ | … | ⑥ | … |
| 小正方形的个数 | 2 | 5 | 9 | 14 | … | 27 | … |
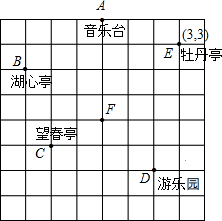 多多和爸爸、妈妈周末到公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道牡丹园的坐标为(3,3),请你帮他建立平面直角坐标系(画在图中)并求出其它各景点的坐标?
多多和爸爸、妈妈周末到公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道牡丹园的坐标为(3,3),请你帮他建立平面直角坐标系(画在图中)并求出其它各景点的坐标?
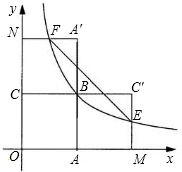 如图,四边形OABC是面积为4的正方形,函数y1=$\frac{k}{x}$(x>0)的图象经过点B.
如图,四边形OABC是面积为4的正方形,函数y1=$\frac{k}{x}$(x>0)的图象经过点B.