题目内容
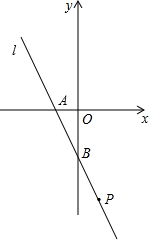 如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足
如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足| OA-2 |
(1)求直线l的解析式;
(2)求过点P的反比例函数解析式;
(3)点C(0,3)在反比例函数图象上是否存在一点D,使以点A、B、C、D为顶点,AC为腰的四边形为梯形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
考点:反比例函数综合题
专题:
分析:(1)根据非负数的性质求得OA和OB的长,即A和B的坐标,利用待定系数法求得直线l的解析式;
(2)AP=2BP,则AB=BP,作PE⊥y轴于点E,证明△AOB≌△PEB,求得PE和OE的长,则P的坐标即可求得,然后利用待定系数法求得反比例函数解析式;
(3)点A、B、C、D为顶点,AC为腰的四边形为梯形,则是梯形ABDC,其中D在第四象限,求得CD的解析式,然后解直线CD的解析式和反比例函数解析式的交点即可求解.
(2)AP=2BP,则AB=BP,作PE⊥y轴于点E,证明△AOB≌△PEB,求得PE和OE的长,则P的坐标即可求得,然后利用待定系数法求得反比例函数解析式;
(3)点A、B、C、D为顶点,AC为腰的四边形为梯形,则是梯形ABDC,其中D在第四象限,求得CD的解析式,然后解直线CD的解析式和反比例函数解析式的交点即可求解.
解答:解:(1)∵
+|OB-3|=0,
∴OA-2=0,OB-3=0,
则OA=2,OB=3,
则A的坐标是(-2,0),B的坐标是(0,-3),
设直线l的解析式是y=kx+b,根据题意得:
,
解得:
,
则直线l的解析式是y=-
x-3;
(2)∵AP=2BP,
∴AB=BP,
作PE⊥y轴于点E.
在△AOB和△PEB中,
,
∴△AOB≌△PEB(AAS),
∴PE=OA=2,BE=OB=,3,即OE=4,
∴P的坐标是(2,-6).
设反比例函数的解析式是y=
,把(2,-6)代入得:k=-12,
则反比例函数的解析式是:y=-
;
(3)点A、B、C、D为顶点,AC为腰的四边形为梯形,
则是梯形ABDC,其中D在第四象限.
设直线CD的解析式是y=-
x+b,把(-2,0)代入解析式得:-3+b=0,
解得:b=3,
则直线CD的解析式是:y=-
x+3.
解方程组
,
解得:
或
(舍去).
则D的坐标是(4,-3).
| OA-2 |
∴OA-2=0,OB-3=0,
则OA=2,OB=3,
则A的坐标是(-2,0),B的坐标是(0,-3),
设直线l的解析式是y=kx+b,根据题意得:
|
解得:
|
则直线l的解析式是y=-
| 3 |
| 2 |
(2)∵AP=2BP,
∴AB=BP,
作PE⊥y轴于点E.
在△AOB和△PEB中,
|
∴△AOB≌△PEB(AAS),
∴PE=OA=2,BE=OB=,3,即OE=4,
∴P的坐标是(2,-6).
设反比例函数的解析式是y=
| k |
| x |

则反比例函数的解析式是:y=-
| 12 |
| x |
(3)点A、B、C、D为顶点,AC为腰的四边形为梯形,
则是梯形ABDC,其中D在第四象限.
设直线CD的解析式是y=-
| 3 |
| 2 |
解得:b=3,
则直线CD的解析式是:y=-
| 3 |
| 2 |
解方程组
|
解得:
|
|
则D的坐标是(4,-3).
点评:本题考查了待定系数法求函数的解析式,以及全等三角形的判定与性质,正确确定点A、B、C、D为顶点,AC为腰的四边形为梯形,是梯形ABDC,其中D在第四象限是关键.

练习册系列答案
相关题目
已知y=2
+
-2,则xy的平方根是( )
| 2-x |
| 2x-4 |
| A、±2 | ||
B、±
| ||
C、±
| ||
| D、不存在 |
从长度分别为2,4,6,7的四条线段随机取三条,能构成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
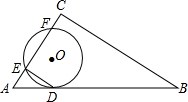 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连接DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连接DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.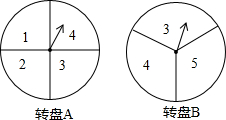 甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区内标上数字(如图所示),指针的位置固定,游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数时,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜,如果指针落在分割线上,则需重新转动转盘.
甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区内标上数字(如图所示),指针的位置固定,游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数时,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜,如果指针落在分割线上,则需重新转动转盘.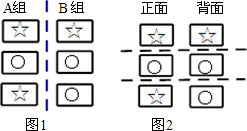 有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上☆○☆,B组的卡片上分别画上☆○○,如图1所示.
有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上☆○☆,B组的卡片上分别画上☆○○,如图1所示.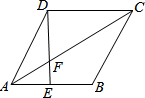 如图,?ABCD中,AE:EB=2:3,DE交AC于F.
如图,?ABCD中,AE:EB=2:3,DE交AC于F.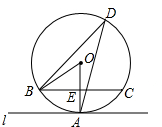 如图,直线l与半径为1的⊙O相切于点A,弦BC∥l,D为圆上一点,∠ADB=30°,连接OB、OA,OA交BC于点E.
如图,直线l与半径为1的⊙O相切于点A,弦BC∥l,D为圆上一点,∠ADB=30°,连接OB、OA,OA交BC于点E.