题目内容
从长度分别为2,4,6,7的四条线段随机取三条,能构成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法,三角形三边关系
专题:
分析:将所有组合列举出来,找到两边之和大于第三边的组合,再利用概率公式解答.
解答:解:从长度分别为2,4,6,7的四条线段随机取三条,可得
2,4,6,2+4=6,不能构成三角形;
2,4,7,2+4<7,不能构成三角形;
2,6,7,2+6>7,能构成三角形;
4,6,7,4+6>7,能构成三角形.
则P(能构成三角形)=
=
.
故选D.
2,4,6,2+4=6,不能构成三角形;
2,4,7,2+4<7,不能构成三角形;
2,6,7,2+6>7,能构成三角形;
4,6,7,4+6>7,能构成三角形.
则P(能构成三角形)=
| 2 |
| 4 |
| 1 |
| 2 |
故选D.
点评:本题考查了三角形三边关系及概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
若α,β是方程x2-2x-3=0的两个实数根,则α+β的值是( )
| A、2 | B、-2 | C、3 | D、-3 |
 如图,五边形ABCDE为正五边形,以下结论正确的是( )
如图,五边形ABCDE为正五边形,以下结论正确的是( )| A、它的内角和为900° |
| B、它的外角和为540° |
| C、它共有两条对角线 |
| D、它共用五条对称轴 |
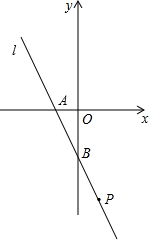 如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足
如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足
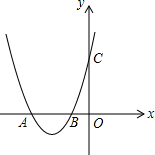 已知:如图,抛物线C1:y=ax2+4ax+c的图象开口向上,与x轴交于点A、B(A在B的左边),与y轴交于点C,顶点为P,AB=2,且OA=OC.
已知:如图,抛物线C1:y=ax2+4ax+c的图象开口向上,与x轴交于点A、B(A在B的左边),与y轴交于点C,顶点为P,AB=2,且OA=OC.
 将表示下列事件发生的概率的字母标在图中:
将表示下列事件发生的概率的字母标在图中: