题目内容
18.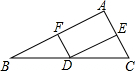 如图,点D是BC的中点,DE垂直平分AC,垂足为E,F是BA的中点,求证:DF是AB的垂直平分线.
如图,点D是BC的中点,DE垂直平分AC,垂足为E,F是BA的中点,求证:DF是AB的垂直平分线.
分析 连接AD,根据垂直平分线的性质得到AD=DC,由BD=CD,等量代换得到AD=BD,推出△ADF≌△BDF,根据全等三角形的性质得到∠AFD=∠BFD,然后根据平角的定义即可得到结论.
解答 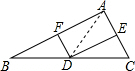 证明:连接AD,
证明:连接AD,
∵DE垂直平分AC,
∴AD=DC,
∵点D是BC的中点,
∴BD=CD,
∴AD=BD,
在△ADF与△BDF中,
$\left\{\begin{array}{l}{AF=BF}\\{DF=DF}\\{AD=BD}\end{array}\right.$,
∴△ADF≌△BDF,
∴∠AFD=∠BFD,
∵∠AFD+∠BFD=180°,
∴∠AFD=∠BFD=90°,
∴DF⊥AB,
∴DF是AB的垂直平分线.
点评 本题考查了线段的垂直平分线的判定和性质,全等三角形的判定和性质,垂直的定义,熟练掌握线段的垂直平分线的性质是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
13.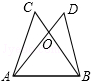 如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
 如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
如图,AD=BC,AC=BD,则下列结论中,不正确的是( )| A. | OA=OB | B. | OC=OD | C. | ∠C=∠D | D. | ∠OAB=∠DBA |
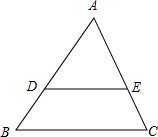 如图,$\frac{AD}{DB}$=$\frac{AE}{EC}$=2,求$\frac{AB}{DB}$、$\frac{AE}{AC}$的值.
如图,$\frac{AD}{DB}$=$\frac{AE}{EC}$=2,求$\frac{AB}{DB}$、$\frac{AE}{AC}$的值.
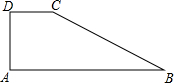 如图,四边形ABCD中,CD∥AB,AD⊥DC,DC=5,CB=15,AB=17.则四边形ABCD的面积为99.
如图,四边形ABCD中,CD∥AB,AD⊥DC,DC=5,CB=15,AB=17.则四边形ABCD的面积为99.