题目内容
8.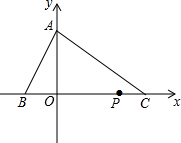 在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.
在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.(1)求点B的坐标;
(2)点P的运动时间为t,三角形AOP的面积为S,用含t的代数式表示S;
(3)若点D在y轴上,是否存在点P,使以D、O、P为顶点的三角形与△AOB全等?若存在,直接写出点D坐标;若不存在,请说明理由.
分析 (1)△ABO和△ACO是同高的三角形,由S△AOC=3S△AOB可知CO=3BO,根据C点坐标可得B点坐标;
(2)根据P的运动速度和时间可得CP=t,进而可得PO=6-t或t-6,然后再利用三角形的面积公式可得出;
(3)此题要分两种情况进行讨论,①当OP=OA时,②当PO=BO时,分别表示出点D坐标.
解答  解:(1)∵点C坐标(6,0),S△AOC=3S△AOB.
解:(1)∵点C坐标(6,0),S△AOC=3S△AOB.
∴B(-2,0);
(2)∵点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,
∴当点P在线段CO上时,点P的运动时间为t,则PO=6-t,
∵点A坐标(0,4),
∴三角形AOP的面积S=$\frac{1}{2}×$4×(6-t)=12-2t;
当点P在O点左侧时,点P的运动时间为t,则PO=t-6,
∵点A坐标(0,4),
∴三角形AOP的面积S=$\frac{1}{2}×$4×(t-6)=2t-12;
综上所述:S=12-2t(0≤t<6),S=2t-12(t>6);
(3)存在,
①当OP=OA时,D(0,2),(0,-2),
②当PO=BO时,D(0,4),(0,-4).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | 3x2•2x=6x3 | B. | x6÷x3=x2 | C. | (3a)2=3a2 | D. | (a+b)2=a2+b2 |
18.下表中每行所给的三个数a、b、c均满足a<b<c,则根据表中已有数据的规律,可得出:当a=20时,b=99,c=101
| 6,8,10 | 8,15,17 | 10,24,26 | … | 20,b,c |
| 62+82=102 | 82+152=172 | 102+242=262 | … | 202+b2=c2 |
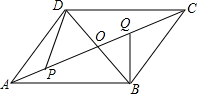 ?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.
?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.