题目内容
19.某企业加工一台大型机械设备润滑用油90千克,用油的重复利用率为60%,按此计算,加工一台大型机械设备的实际耗油量为36千克.通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现润滑用油量每减少1千克,用油量的重复利用率增加1.6%,这样加工一台大型机械设备的实际耗油量下降到12千克,问技术革新后,加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少?分析 设乙车间加工一台大型机械设备润滑用油量为x千克,由“实际耗油量下降到12千克”列方程得x×[1-(90-x)×1.6%-60%]=12,解方程求解即可.
解答 解:设乙车间加工一台大型机械设备润滑用油量为x千克,
由题意得:x×[1-(90-x)×1.6%-60%]=12,
整理得:x2-65x-750=0,
因式分解得:(x-75)(x+10)=0,
解得x1=75,x2=-10(舍去)
∴用油的重复利用率:(90-75)×1.6%+60%=84%.
答:技术革新后,乙车间加工一台大型机械设备润滑用油量是75千克,用油的重复利用率是84%.
点评 此题考查了列一元二次方程在实际中的应用;同时考查了学生分析问题、解决问题的能力.分析数量关系、探究等量关系是列方程解应用题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
10.已知下列命题,其中真命题的个数是( )
①若a2=b2,则a=b;
②对角线互相垂直且相等的四边形是正方形;
③两组对角分别相等的四边形是平行四边形;
④在反比例函数y=$\frac{2}{x}$中,如果函数值y<1时,那么自变量x>2.
①若a2=b2,则a=b;
②对角线互相垂直且相等的四边形是正方形;
③两组对角分别相等的四边形是平行四边形;
④在反比例函数y=$\frac{2}{x}$中,如果函数值y<1时,那么自变量x>2.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9.反比例函数y=$\frac{2}{x}$的图象位于平面直角坐标系的( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二象限 | D. | 第三、四象限 |
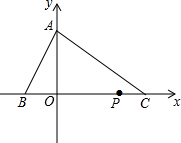 在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.
在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.