题目内容
18.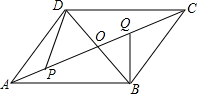 ?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.
?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.(1)线段PQ的长为12;
(2)设△PDO的面积为S1,△QBO的面积为S2,S1+S2的值是否发生变化?若不变,求出这个不变的值;若变化,请说明随着AP的增大,S1+S2的值是如何变化的;
(3)DP+BQ的最小值是12.
分析 (1)由平行四边形的性质得出OA=OC,OB=OD=$\frac{1}{2}$BD=6,由含30°角的直角三角形的性质得出OA=2OD,求出PQ=OA即可;
(2)由OD=OB得出S△ODQ=S△OBQ,由AP=OQ,得出S△APD=S△OQD,求出S1+S2=S△DPQ=S△AOD,再由勾股定理求出AD,即可得出结果;
(3)当AP=OP时,DP+BQ的值最小,此时P为OA的中点,由直角三角形斜边上的中线性质得出DP、BQ,即可得出结果.
解答 解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD=$\frac{1}{2}$BD=6,
∵∠AOD=60°,∠ADO=90°,
∴∠OAD=30°,
∴OA=2OD=12,
∵AP=OQ,
∴OP+OQ=OP+AP=OA=12,
即PQ=12;
故答案为:12;
(2)S1+S2的值不变,S1+S2=18$\sqrt{3}$;理由如下:
如图所示,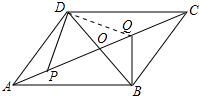 连结DQ,
连结DQ,
∵四边形ABCD是平行四边形,
∴OD=OB,
∴S△ODQ=S△OBQ,
∵AP=OQ,
∴S△APD=S△OQD,
∴S1+S2=S△DPQ=S△AOD,
在Rt△AOD中,由勾股定理得:
AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$
∴S1+S2=S△AOD=$\frac{1}{2}$AD•OD=$\frac{1}{2}$×6$\sqrt{3}$×6=18$\sqrt{3}$;
(3)DP+BQ最小值是12;理由如下:
当AP=OP时,DP+BQ的值最小,此时P为OA的中点,
∵∠ADO=90°,
∴DP=$\frac{1}{2}$OA=6,
同理BQ=6,
∴DP+BQ的最小值=6+6=12;
故答案为:12.
点评 本题是四边形综合题目,考查了平行四边形的性质、含30°角的直角三角形的性质、勾股定理、直角三角形斜边上的中线性质、三角形面积的计算等知识;本题难度较大,综合性强,特别是(2)(3)中,需要运用勾股定理、直角三角形斜边上的中线性质等知识才能得出结果.

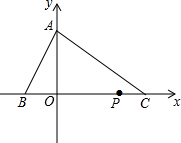 在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.
在平面直角坐标中,点A坐标(0,4),点C坐标(6,0),点B在x轴负半轴上,点P从点C出发,以1个单位/秒的速度沿x轴负方向运动,且S△AOC=3S△AOB.