题目内容
抛物线y=-3x2+2x-1与坐标轴的交点个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:抛物线与x轴的交点
专题:计算题
分析:先根据判别式的值得到△=-8<0,根据△=b2-4ac决定抛物线与x轴的交点个数得到抛物线与x轴没有交点,由于抛物线与y轴总有一个交点,所以抛物线y=-3x2+2x-1与坐标轴的交点个数为1.
解答:解:∵△=22-4×(-3)×(-1)=-8<0,
∴抛物线与x轴没有交点,
而抛物线y=-3x2+2x-1与y轴的交点为(0,-1),
∴抛物线y=-3x2+2x-1与坐标轴的交点个数为1.
故选B.
∴抛物线与x轴没有交点,
而抛物线y=-3x2+2x-1与y轴的交点为(0,-1),
∴抛物线y=-3x2+2x-1与坐标轴的交点个数为1.
故选B.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
若x2-6x+11=(x-m)2+n,则m,n的值分别是( )
| A、m=3,n=-2 |
| B、m=3,n=2 |
| C、m=-3,n=-2 |
| D、m=-3,n=2 |
某商场利用转盘进行有奖促销,转盘扇形区域的圆心角及奖品设置如下表:
小英有一次转转盘的机会,她能获得奖品为学习机的概率是( )
| 特等奖 | 一等奖 | 二等奖 | 三等奖 | 鼓励奖 | |
| 圆心角 | 1° | 10° | 60° | 90° | 199° |
| 奖品 | 冰箱 | 彩电 | 学习机 | 自行车 | 笔记本 |
A、
| ||
B、
| ||
C、
| ||
D、
|
使等式
=
•
成立的x的取值范围是( )
| x(x-2) |
| x |
| x-2 |
| A、x≠2 | B、x≥0 |
| C、x>2 | D、x≥2 |
 如图,有三个矩形,其中是相似图形的是( )
如图,有三个矩形,其中是相似图形的是( )| A、甲和乙 | B、甲和丙 |
| C、乙和丙 | D、甲、乙和丙 |
已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数y=
的图象上的三点,且x1<x2<0<x3,则y1,y2,y3的大小关系是( )
| 7 |
| x |
| A、y3<y2<y1 |
| B、y1<y2<y3 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
下列条件中,不能判定四边形ABCD是平行四边形的是( )
| A、AB=CD,AD=BC |
| B、AB∥CD,AB=CD |
| C、AB=CD,AD∥BC |
| D、AB∥CD,AD∥BC |
 如图,已知双曲线
如图,已知双曲线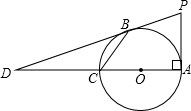 如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且
如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且