题目内容
某商场利用转盘进行有奖促销,转盘扇形区域的圆心角及奖品设置如下表:
小英有一次转转盘的机会,她能获得奖品为学习机的概率是( )
| 特等奖 | 一等奖 | 二等奖 | 三等奖 | 鼓励奖 | |
| 圆心角 | 1° | 10° | 60° | 90° | 199° |
| 奖品 | 冰箱 | 彩电 | 学习机 | 自行车 | 笔记本 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概率
专题:
分析:直接利用她能获得奖品为学习机在扇形统计图中所占圆心角度数,进而除以360得出她能获得奖品为学习机的概率.
解答:解:由题意可得出:她能获得奖品为学习机所占圆心角为60°,
∴她能获得奖品为学习机的概率是:
=
.
故选:A.
∴她能获得奖品为学习机的概率是:
| 60 |
| 360 |
| 1 |
| 6 |
故选:A.
点评:此题主要考查了几何概率,直接利用概率公式求出是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
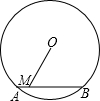 如图,已知⊙O的半径为5,弦AB=7,M是AB上任意一点,则线段OM的长不可能是( )
如图,已知⊙O的半径为5,弦AB=7,M是AB上任意一点,则线段OM的长不可能是( )| A、3.5 | B、4.5 | C、4 | D、5 |
若x2+6x+m2是一个完全平方式,则实数m的值是( )
| A、3 | B、-3 |
| C、±3 | D、以上都不对 |
某平行四边形的对角线长分别为a,b,一边长为12,则a与b的值可能是( )
| A、6和12 | B、10和14 |
| C、18和20 | D、10和34 |
已知ab<0,化简
的结果是( )
| ab2 |
A、b
| ||
B、-b
| ||
C、b
| ||
D、-b
|
下列方程中,不是一元二次方程的是( )
A、
| ||||
B、
| ||||
| C、0.1x2-x+1=0 | ||||
D、
|
抛物线y=-3x2+2x-1与坐标轴的交点个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且BE=AC.求证:∠DEC=45°.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且BE=AC.求证:∠DEC=45°.