题目内容
9．已知：点A（x1，y1），B（x2，y2），C（x3，y3）是函数y=-$\frac{3}{x}$图象上的三点，且x1＜0＜x2＜x3，则y1，y2，y3的大小关系是（ ）| A． | y1＜y2＜y3 | B． | y2＜y3＜y1 | C． | y3＜y2＜y1 | D． | 无法确定 |
分析 根据反比例函数图象的增减性进行分析解答即可．
解答 解：根据反比例函数的性质可知，函数数y=-$\frac{3}{x}$的图象在二、四象限，由于 x1＜0＜x2＜x3，因此 y1＞0，y2＜0，y3＜0，所以 y1最大；
在第四象限中，y随x的增大而增大，因为 x2＜x3，所以 y2＜y3，所以 y2＜y3＜y1，
故选：B．
点评 本题考查了反比例函数图象上点的坐标特征．本题还可以画出反比例函数 y=-$\frac{3}{x}$图象，在图象上找出A，B，C三点的大体位置，确定它们的纵坐标，即得出 y1，y2，y3的大小．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
20．
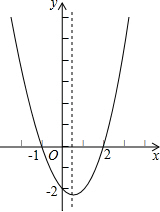二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（ ）
二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（ ）| A． | 函数有最小值 | B． | 对称轴是直线x=$\frac{1}{2}$ | ||
| C． | 当x＜$\frac{1}{2}$时，y随x的增大而减小 | D． | 当-1＜x＜3时，y＞0 |
17．下列计算，正确的是（ ）
| A． | 3a2×2a2=6a2 | B． | （2x-1）•3x2y=6x3y-1 | ||
| C． | （-ab）3÷（-ab）=a2b2 | D． | （$\frac{1}{3}$）0×3=0 |
4．下列各组数中，互为相反数的一组是（ ）
| A． | -2与$\sqrt{（-2）^{2}}$ | B． | -2与$\root{3}{-8}$ | C． | 2与$\sqrt{-4}$ | D． | $\sqrt{1{0}^{-4}}$与2 |
如图，在平面直角坐标系中，Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上，OA=1，∠OBA=30°，将△AOB绕点A顺时针旋转，使AB的对应边AD恰好落在x轴上，点O的对应点C落在函数y=$\frac{k}{x}$（x＞0）的图象上，则k的值为$\frac{3\sqrt{3}}{4}$．
1．若a为有理数，则a的倒数$\frac{1}{a}$（ ）
| A． | 一定是实数 | B． | 是无理数 | ||
| C． | 不存在 | D． | 当a≠0时，$\frac{1}{a}$一定是有理数 |