题目内容
17.已知直线y=kx+b经过点(-1,4)和(2,1).(1)求直线的表达式;
(2)求直线和两坐标轴围成的三角形的面积.
分析 (1)将点的坐标代入求出k和b的值,即可得出函数解析式;
(2)根据解析式分别求出直线与x轴和y轴的交点,根据三角形的面积公式求解.
解答 解:(1)∵直线y=kx+b经过点(-1,4)和点(2,1),
∴$\left\{\begin{array}{l}{-k+b=4}\\{2k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$.
则直线的表达式为y=-x+3;
(2)如图所示:
直线与坐标轴的交点为(3,0),(0,3),
面积为:$\frac{1}{2}$×3×3=$\frac{9}{2}$.
点评 本题考查了待定系数法求一次函数的解析式,一次函数的图象,一次函数图象上点的坐标特征,三角形的面积,掌握待定系数法求函数解析式的方法与步骤是解决问题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
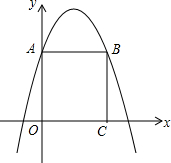 如图,在平面直角坐标系中,正方形ABCD的边长为2,抛物线y=ax2+bx+c经过A,B两点,且与x轴的一个交点坐标是(-$\frac{2}{9}$,0),求这个抛物线的解析式.
如图,在平面直角坐标系中,正方形ABCD的边长为2,抛物线y=ax2+bx+c经过A,B两点,且与x轴的一个交点坐标是(-$\frac{2}{9}$,0),求这个抛物线的解析式.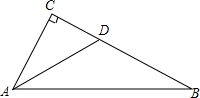 如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.
如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.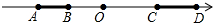 如图.在数轴上有A、B.、C、D四个点.且AB=2,CD=4.已知A表示的数是-10,C表示的数是16,若线段AB以每秒6个单位长度的速度向右运动,同时线段CD以每秒2个单位长度向左运动.
如图.在数轴上有A、B.、C、D四个点.且AB=2,CD=4.已知A表示的数是-10,C表示的数是16,若线段AB以每秒6个单位长度的速度向右运动,同时线段CD以每秒2个单位长度向左运动.