题目内容
14.将函数y=ax2(a≠0)与直线y=kx-2相交于A、B两点,A的坐标是(-1,-1).求:(1)a,k的值;
(2)B点的坐标;
(3)△OAB的面积.
分析 (1)将A点分别代入y=ax2(a≠0)与y=kx-2中,即可求出a,k的值即可;
(2)将两函数解析式联立求出交点坐标即可;
(3)画出图象进而分割得出S△OAB=S△OAG+S△OBG进而得出答案.
解答 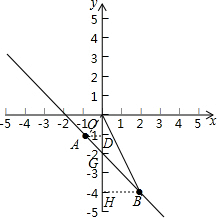 解:(1)∵函数y=ax2过(-1,-1),
解:(1)∵函数y=ax2过(-1,-1),
∴a=-1,
将(-1,-1)代入y=kx-2得:
-1=-k-2,
解得:k=-1;
(2)∵a=-1,k=-1,
∴y=-x-2,y=-x2,
∴$\left\{\begin{array}{l}{y=-x-2}\\{y=-{x}^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=-1}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=-4}\end{array}\right.$,
故点B的坐标为:(2,-4);
(3)设直线AB交y轴于点G,过点A、B向y轴作垂线段AD、BH,垂足分别为:D、H,
则AD=1,BH=2,OG=2,
∴S△OAB=S△OAG+S△OBG=$\frac{1}{2}$OG×DA+$\frac{1}{2}$GO×BH=3.
点评 此题主要考查了二次函数的性质以及三角形面积计算等知识,正确分割三角形进而求出面积是解题关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
4.某班女生有n人,男生人数是女生人数的$\frac{3}{2}$,则全班人数是( )
| A. | $\frac{3}{2}$n | B. | $\frac{2}{3}$n | C. | $\frac{5}{2}$n | D. | $\frac{2}{5}$n |
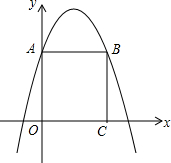 如图,在平面直角坐标系中,正方形ABCD的边长为2,抛物线y=ax2+bx+c经过A,B两点,且与x轴的一个交点坐标是(-$\frac{2}{9}$,0),求这个抛物线的解析式.
如图,在平面直角坐标系中,正方形ABCD的边长为2,抛物线y=ax2+bx+c经过A,B两点,且与x轴的一个交点坐标是(-$\frac{2}{9}$,0),求这个抛物线的解析式.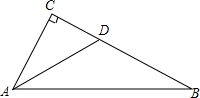 如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.
如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.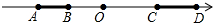 如图.在数轴上有A、B.、C、D四个点.且AB=2,CD=4.已知A表示的数是-10,C表示的数是16,若线段AB以每秒6个单位长度的速度向右运动,同时线段CD以每秒2个单位长度向左运动.
如图.在数轴上有A、B.、C、D四个点.且AB=2,CD=4.已知A表示的数是-10,C表示的数是16,若线段AB以每秒6个单位长度的速度向右运动,同时线段CD以每秒2个单位长度向左运动.