题目内容
16.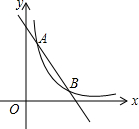 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,6),B(a,2)两点.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,6),B(a,2)两点.(1)求一次函数与反比例函数的解析式;
(2)直接写出y1>y2时x的取值范围.
分析 (1)先A点坐标代入y2=$\frac{m}{x}$(x>0)求出m确定反比例函数解析式为y2=$\frac{6}{x}$;在把B(a,2)代入y2=$\frac{6}{x}$求出a,确定B点坐标为(3,2),然后利用待定系数法确定一次函数解析式;
(2)观察函数图象,当1<x<3时,一次函数图象都在反比例函数图象上方.
解答 解:(1)把A(1,6)代入y2=$\frac{m}{x}$得m=1×6=6,
所以反比例函数解析式为y2=$\frac{6}{x}$;
把B(a,2)代入y2=$\frac{6}{x}$得2a=6,解得a=3,
所以B点坐标为(3,2),
把A(1,6)和B(3,2)代入y1=kx+b得$\left\{\begin{array}{l}{k+b=6}\\{3k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$,
所以一次函数解析式为y1=-2x+8;
(2)当1<x<3时,y1>y2.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6. 如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
 如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.| A. | 400 | B. | 500 | C. | 300 | D. | 750 |
11.如果关于x的一元二次方程x2-4x+k=0有两个相等的实数根,那么k的值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
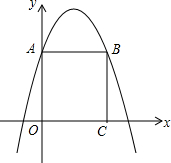 如图,在平面直角坐标系中,正方形ABCD的边长为2,抛物线y=ax2+bx+c经过A,B两点,且与x轴的一个交点坐标是(-$\frac{2}{9}$,0),求这个抛物线的解析式.
如图,在平面直角坐标系中,正方形ABCD的边长为2,抛物线y=ax2+bx+c经过A,B两点,且与x轴的一个交点坐标是(-$\frac{2}{9}$,0),求这个抛物线的解析式.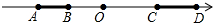 如图.在数轴上有A、B.、C、D四个点.且AB=2,CD=4.已知A表示的数是-10,C表示的数是16,若线段AB以每秒6个单位长度的速度向右运动,同时线段CD以每秒2个单位长度向左运动.
如图.在数轴上有A、B.、C、D四个点.且AB=2,CD=4.已知A表示的数是-10,C表示的数是16,若线段AB以每秒6个单位长度的速度向右运动,同时线段CD以每秒2个单位长度向左运动.