题目内容
13. 如图,已知BE=CD,要使△ABE≌△ACD,要添加一个条件是∠B=∠C.(只填一种情况).
如图,已知BE=CD,要使△ABE≌△ACD,要添加一个条件是∠B=∠C.(只填一种情况).
分析 此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.
解答 解:∠B=∠C,
理由是:∵在△ABE和△ACD中
$\left\{\begin{array}{l}{∠B=∠C}\\{∠A=∠A}\\{BE=CD}\end{array}\right.$
∴△ABE≌△ACD(AAS),
故答案为:∠B=∠C.
点评 本题考查了全等三角形的判定定理的应用,能熟记判定定理的内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
3.已知,点A(-6,y1)和点B(1,y2)都在直线y=-$\frac{1}{2}$x-1上,那么y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不确定 |
18.已知直线y=kx(x≠0)经过点(-1,2),则此正比例函数的解析式为( )
| A. | y=-2x | B. | y=2x | C. | y=-$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
2.下列等式一定成立的是( )
| A. | a2×a5=a10 | B. | $\sqrt{a+b}=\sqrt{a}+\sqrt{b}$ | C. | (-a3)4=a12 | D. | $\sqrt{a^2}=a$ |
4.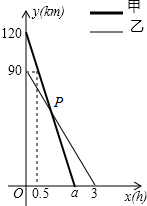 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )| A. | A、C两村间的距离为120km | |
| B. | 点P的坐标为(1,60) | |
| C. | 点P的意义表示经过1小时甲与乙相遇且距C村60km | |
| D. | 乙在行驶过程中,仅有一次机会距甲10km |
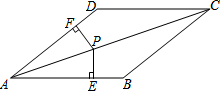 如图,在四边形ABCD中,AB∥CD,∠B=∠D.
如图,在四边形ABCD中,AB∥CD,∠B=∠D. 如图,边长为4的正方形ABCD中对角线AC、BD相交于点O,OE⊥CD,则OE=2.
如图,边长为4的正方形ABCD中对角线AC、BD相交于点O,OE⊥CD,则OE=2.