题目内容
4.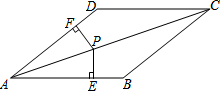 如图,在四边形ABCD中,AB∥CD,∠B=∠D.
如图,在四边形ABCD中,AB∥CD,∠B=∠D.(1)求证:四边形ABCD为平行四边形;
(2)若点P为对角线AC上的一点,PE⊥AB于E,PF⊥AD于F,且PE=PF,求证:四边形ABCD是菱形.
分析 (1)根据平行线的性质和平行四边形的判定证明即可;
(2)根据角平分线的性质和菱形的判定证明即可.
解答 证明:(1)∵AB∥CD,
∴∠DCA=∠BAC,
在△ADC与△ABC中,
$\left\{\begin{array}{l}{∠B=∠D}\\{∠DCA=∠BAC}\\{AC=AC}\end{array}\right.$,
∴△ADC≌△ABC(AAS),
∴AB=DC,
∵AB∥CD,
∴四边形ABCD为平行四边形;
(2)∵四边形ABCD为平行四边形,
∴∠DAB=∠DCB,
∵PE⊥AB于E,PF⊥AD于F,且PE=PF,
∴∠DAC=∠BAC=∠DCA=∠BCA,
∴AB=BC,
∴四边形ABCD是菱形.
点评 本题考查了菱形的判定与性质.菱形的判定方法有五多种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列分式中最简分式为( )
| A. | $\frac{4}{2x}$ | B. | $\frac{2x}{{x}^{2}+1}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{1-x}{x-1}$ |
9.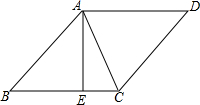 如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )
如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )
 如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )
如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )| A. | 24 | B. | 36 | C. | 48 | D. | 4.8 |
16.计算:(ab3)2=( )
| A. | a2b2 | B. | a2b3 | C. | ab6 | D. | a2b6 |
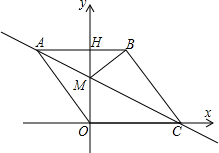 如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM. 如图,已知BE=CD,要使△ABE≌△ACD,要添加一个条件是∠B=∠C.(只填一种情况).
如图,已知BE=CD,要使△ABE≌△ACD,要添加一个条件是∠B=∠C.(只填一种情况).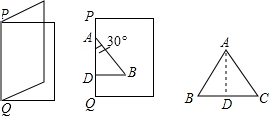 如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.
如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.