题目内容
4.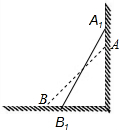 如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.
如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.
分析 梯子的长是不变的,只要利用勾股定理解出梯子滑动前和滑动后的所构成的两直角三角形,分别得出AO,A1O的长即可.
解答  解:在Rt△ABO中,根据勾股定理知,AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=4(m),
解:在Rt△ABO中,根据勾股定理知,AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=4(m),
在Rt△A1B1O中,由题意可得:B1O=1.4(m),
根据勾股定理知,A1O=$\sqrt{{5}^{2}-1.{4}^{2}}$=4.8(m),
所以AA1=A1O-AO=0.8(米).
故答案为:0.8.
点评 本题考查了勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
14.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
| A. | 当a<1时,点B在⊙A外 | B. | 当1<a<5时,点B在⊙A内 | ||
| C. | 当a<5时,点B在⊙A内 | D. | 当a>5时,点B在⊙A外 |
12.抛物线y=x2-2的顶点坐标为( )
| A. | (0,-2) | B. | (-2,0) | C. | (0,2) | D. | (2,0) |
16.若一直角三角形的两边长分别为2和4,则第三边长为( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{3}$或2$\sqrt{5}$ | D. | 6 |
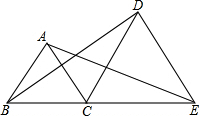 点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB.
点B、C、E在同一直线上,△ABC和△DCE均为等边三角形,连结AE,DB,求证:AE=DB. 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,其中A(1,-3),B(3,-4),C(4,-1);
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,其中A(1,-3),B(3,-4),C(4,-1); 如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:∠DCE=∠MDF(答案不唯一).
如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:∠DCE=∠MDF(答案不唯一).
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3).请按下列要求画图:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3).请按下列要求画图: