题目内容
14. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3).请按下列要求画图:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3).请按下列要求画图:(1)将△ABC绕点O逆时针旋转90°得到△A1B1C1,画出△A1B1C1;
(2)△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
分析 (1)利用网格特点和旋转的性质画出点A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;
(2)根据关于原点中心对称的点的坐标特征写出点A2、B2、C2的坐标,然后描点即可.
解答 解:(1)如图,将△A1B1C1为所作;
(2)如图,△A2B2C2为所作.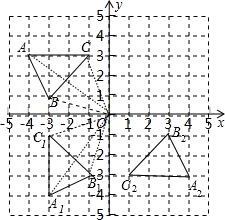
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
5.小李将1000元钱存入银行,年利率为x,第二年他把本息和全部存入银行,两年后不计利息税,他得到本息共a元,则依题意可列方程为( )
| A. | 1000(x+x)=a | B. | 1000(1-2x)=a | C. | 1000(1+x)2=a | D. | 1000(1+2x)2=a |
2.下列语句是命题的是( )
| A. | 相等的角是对顶角 | B. | 同位角相等,两直线平行吗? | ||
| C. | 作∠AOB的平分线OC | D. | 延长线AB到C使AC=2AB |
6.已知△ABC的三个内角∠A,∠B,∠C满足∠A=∠B=∠C,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 等边三角形 | D. | 钝角三角形 |
3.以下命题中,正确的是( )
| A. | 一腰相等的两个等腰三角形全等. | |
| B. | 等腰三角形底边上的任意一点到两腰距离之和都大于一腰上的高. | |
| C. | 有一角相等和底边相等的两个等腰三角形全等. | |
| D. | 等腰三角形的角平分线、中线和高共7条或3条. |
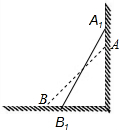 如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.
如图所示,一架5米长的消防梯子斜靠在一竖直的墙AC上,梯足(点B)离墙底端(C点)的距离为3米,如果梯足内移1.6米至点B处,则梯子顶端沿墙垂直上移0.8米.