题目内容
17.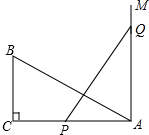 如图,Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.
如图,Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.
分析 本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AQ=AC=10cm,②Rt△QAP≌Rt△BCA,此时AQ=BC=5cm.
解答 解:根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,
$\left\{\begin{array}{l}{AP=BC}\\{PQ=AB}\end{array}\right.$
∴Rt△ABC≌Rt△QPA(HL),
即AQ=AC=10cm;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,
$\left\{\begin{array}{l}{AP=AC}\\{PQ=AB}\end{array}\right.$,
∴Rt△QAP≌Rt△BCA(HL),
即AQ=BC=5cm,
综上所述,当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.
故答案为10cm或5cm.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.二元一次方程组$\left\{\begin{array}{l}{x+2y=2}\\{2x+y=-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$ |
 已知:如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,求∠M.
已知:如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,求∠M. 如图,△ABD与△ACE中,AB=AC,∠ACE+∠ABD=180°,BD=CE,BC延长线交ED于F.
如图,△ABD与△ACE中,AB=AC,∠ACE+∠ABD=180°,BD=CE,BC延长线交ED于F.