题目内容
9. 如图,△ABD与△ACE中,AB=AC,∠ACE+∠ABD=180°,BD=CE,BC延长线交ED于F.
如图,△ABD与△ACE中,AB=AC,∠ACE+∠ABD=180°,BD=CE,BC延长线交ED于F.(1)求证:∠DBF=∠ECF;
(2)图中是否存在与DF相等的线段?若存在,请找出,并加以证明;若不存在,说明理由.
分析 (1)根据∠ACE+∠ABC+∠DBF=180°和∠ACB+∠ACE+∠ECF=180°结合AB=AC即可证明.
(2)结论:DF=EF,如图延长CF使得CM=BF,由△DBF≌△ECM,得DF=ME,∠DFB=∠M由此即可证明.
解答 (1)证明:∵∠ACE+∠ABD=180°,∠ABD=∠ABC+∠DBF,
∴∠ACE+∠ABC+∠DBF=180°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACB+∠ACE+∠ECF=180°,
∴∠DBF=∠ECF.
(2)结论:DF=EF.
理由: 如图延长CF使得CM=BF,
如图延长CF使得CM=BF,
在△DBF和△ECM中,
$\left\{\begin{array}{l}{BD=CE}\\{∠DBF=∠ECM}\\{BF=CM}\end{array}\right.$,
∴△DBF≌△ECM,
∴DF=ME,∠DFB=∠M,
∵∠DFB=∠MFE,
∴∠M=∠MFE,
∴ME=EF,
∴DF=EF.
点评 本题考查全等三角形的判定和性质,等腰三角形的性质、等角的补角相等,添加辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
14. 如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
 如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )| A. | 5 | B. | $\frac{15}{2}$ | C. | $\frac{25}{4}$ | D. | $\frac{20}{3}$ |
19.下列调查适合作抽样调查的是( )
| A. | 了解巫溪网“今日巫溪”栏目的阅览率 | |
| B. | 了解某甲型H1N1确诊病人同机乘客的健康状况 | |
| C. | 了解某班每个学生家庭电脑的数量 | |
| D. | 对“歼20”隐形战斗机零部件的检查 |
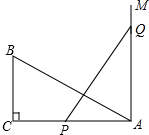 如图,Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.
如图,Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.
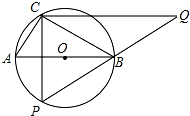 如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.
如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.