题目内容
10.计算:($\sqrt{3}$-1)2-$\frac{2}{\sqrt{3}+1}$+$\frac{6}{\sqrt{3}}$.分析 根据完全平方公式、分母有理化,把二次根式化为最简二次根式,再合并同类二次根式即可.
解答 解:原式=3+1-2$\sqrt{3}$-$\frac{2(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$+$\frac{6\sqrt{3}}{\sqrt{3}•\sqrt{3}}$
=4-2$\sqrt{3}$-2($\sqrt{3}$-1)+2$\sqrt{3}$
=6-2$\sqrt{3}$.
点评 本题考查了二次根式的混合运算,把二次根式化为最简二次根式是解题的关键.

练习册系列答案
相关题目
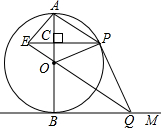 如图,AB是⊙0的直径,BM切⊙0于点B,点P是⊙0上的一个动点(不经过A、B两点),过点0作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ.
如图,AB是⊙0的直径,BM切⊙0于点B,点P是⊙0上的一个动点(不经过A、B两点),过点0作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ.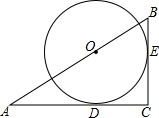 如图,△ABC中,以AB上一点O为圆心的⊙O分别与AC、BC相切于D、E,若AC=4,BC=3,求⊙O的半径.
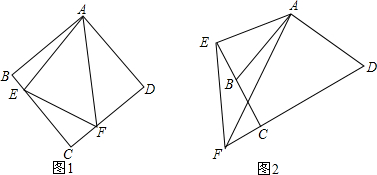
如图,△ABC中,以AB上一点O为圆心的⊙O分别与AC、BC相切于D、E,若AC=4,BC=3,求⊙O的半径.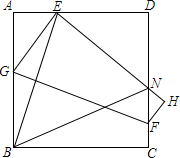 如图,四边形ABCD是正方形,E是AD边上一点,将正方形折叠,使点B与点E重合,FG是折痕,C点落在H上,EH与CD交于点N.求证:∠EBN=45°.
如图,四边形ABCD是正方形,E是AD边上一点,将正方形折叠,使点B与点E重合,FG是折痕,C点落在H上,EH与CD交于点N.求证:∠EBN=45°.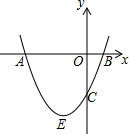 如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A,B,点A在点B的左侧,点A的坐标为A(-3,0),且AB=4.
如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A,B,点A在点B的左侧,点A的坐标为A(-3,0),且AB=4.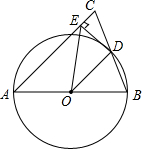 如图,△ABC中,AB=AC,以AB为直径作⊙0,交BC于D,DE⊥AC于E,连接0E.
如图,△ABC中,AB=AC,以AB为直径作⊙0,交BC于D,DE⊥AC于E,连接0E.