题目内容
3.先化简,再求值.(1)$\frac{1}{a+b}$+$\frac{1}{b}$+$\frac{b}{a(a+b)}$,其中a=$\frac{\sqrt{5}+1}{2}$,b=$\frac{\sqrt{5}-1}{2}$.
(2)$\frac{a-2}{{a}^{2}-1}$÷(1-$\frac{2a-3}{a-1}$),其中a=$\sqrt{2}$.
分析 (1)原式通分并利用同分母分式的加法法则计算得到最简结果,把a与b的值代入计算即可求出值;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:(1)原式=$\frac{ab}{ab(a+b)}$+$\frac{a(a+b)}{ab(a+b)}$+$\frac{{b}^{2}}{ab(a+b)}$=$\frac{{a}^{2}+2ab+{b}^{2}}{ab(a+b)}$=$\frac{(a+b)^{2}}{ab(a+b)}$=$\frac{a+b}{ab}$,
当a=$\frac{\sqrt{5}+1}{2}$,b=$\frac{\sqrt{5}-1}{2}$时,原式=$\frac{\frac{\sqrt{5}+1}{2}+\frac{\sqrt{5}-1}{2}}{\frac{\sqrt{5}+1}{2}×\frac{\sqrt{5}-1}{2}}$=$\frac{\sqrt{5}}{1}$=$\sqrt{5}$;
(2)原式=$\frac{a-2}{(a+1)(a-1)}$÷$\frac{a-1-2a+3}{a-1}$=$\frac{a-2}{(a+1)(a-1)}$•$\frac{a-1}{-(a-2)}$=-$\frac{1}{a+1}$,
当a=$\sqrt{2}$时,原式=-$\frac{1}{\sqrt{2}+1}$=-($\sqrt{2}$-1)=1-$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
18.关于二次函数y=-2x2+4x+1,下列说法正确的是( )
| A. | 图象是开口向上的抛物线 | |
| B. | 图象对称轴是直线:x=-1 | |
| C. | 点A(x1,y1)和点B(x2,y2)是图象上的两个点,若x1<x2<-1,则y1<y2 | |
| D. | 图象可由y=-2x2的图象向左平移1个单位,再向下平移3个单位得到 |
12.下列各式计算正确的是( )
| A. | 3a+2b=5 | B. | a5÷a=a4 | C. | (-2a2)3=-6a6 | D. | 3a-2=$\frac{1}{9{a}^{2}}$ |
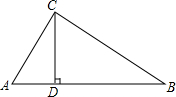 如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于点D,
如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于点D,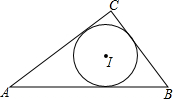 如图,△ABC中,已知AB=8,BC=5,AC=7,则它的内切圆的半径为$\sqrt{3}$.
如图,△ABC中,已知AB=8,BC=5,AC=7,则它的内切圆的半径为$\sqrt{3}$.