题目内容
15.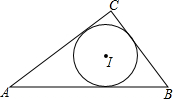 如图,△ABC中,已知AB=8,BC=5,AC=7,则它的内切圆的半径为$\sqrt{3}$.
如图,△ABC中,已知AB=8,BC=5,AC=7,则它的内切圆的半径为$\sqrt{3}$.
分析 作AD⊥BC于D,根据直角三角形的性质和勾股定理求出AD、DC的长,根据三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r计算即可.
解答 解:过点C作CD⊥AB,垂足为D.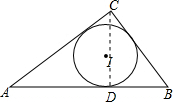
设AD=x,则BD=8-x.
由勾股定理得:CD2=AC2-AD2,CD2=BC2-BD2.
∴72-x2=52-(8-x)2.
解得:x=5.5.
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\frac{5\sqrt{3}}{2}$.
由△ABC的面积=$\frac{1}{2}$×(AB+BC+AC)×r可知:$\frac{1}{2}×(8+5+7)r=\frac{1}{2}×8×\frac{5\sqrt{3}}{2}$.
解得:r=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题主要考查的是勾股定理的定义、三角形的内心,明确三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
6.下列判定正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 两角相等的四边形是梯形 | |
| C. | 四边相等且有一个角是直角的四边形是正方形 | |
| D. | 两条对角线相等且互相垂直的四边形是正方形 |
 如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?
如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?