题目内容
13.计算:$\frac{1}{{x}^{2}+x-1}$-$\frac{2}{{x}^{2}+x+1}$+$\frac{1}{{x}^{2}+x+3}$.分析 原式通分并利用同分母分式的加减法则计算即可得到结果.
解答 解:原式=$\frac{{x}^{2}+x+1-2{x}^{2}-2x+2}{({x}^{2}+x)^{2}-1}$+$\frac{1}{{x}^{2}+x+3}$=$\frac{(-{x}^{2}-x+3)({x}^{2}+x+3)+{x}^{4}+2{x}^{3}+{x}^{2}-1}{({x}^{4}+2{x}^{3}+{x}^{2}-1)({x}^{2}+x+3)}$=$\frac{8}{({x}^{4}+2{x}^{3}+{x}^{2}-1)({x}^{2}+x+3)}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
1.某商店新进货10箱水果,以每箱15千克为标准(不含纸箱重量),超过或不足的千克数分别用正、负数来表示,依据每箱差值大小依次记为A、B、C、D、E五类,见下表:
(1)10箱水果中,最重的一箱比最轻的一箱多4.5千克;
(2)这10箱水果的总重量是153千克;
(3)这批水果有两种销售方式:
甲种:每箱60元;
乙种:按每箱中的水果实际重量计算,每千克4元;
王老师从A、B、D、E四类水果中选择了若干箱,发现用甲种方式购买比用乙种方式购买节约16元,试求王老师各类水果各类水果各购买了几箱(要求写出所有可能)?
| 水果箱的类别 | A | B | C | D | E |
| 与标准质量的差值(单位:千克) | -2 | -1.5 | 0 | 1 | 2.5 |
| 箱数 | 1 | 3 | 1 | 2 | 3 |
(2)这10箱水果的总重量是153千克;
(3)这批水果有两种销售方式:
甲种:每箱60元;
乙种:按每箱中的水果实际重量计算,每千克4元;
王老师从A、B、D、E四类水果中选择了若干箱,发现用甲种方式购买比用乙种方式购买节约16元,试求王老师各类水果各类水果各购买了几箱(要求写出所有可能)?
18.△ABC≌△DEF,且△ABC的周长为18,若AB=5,AC=6,则EF等于( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
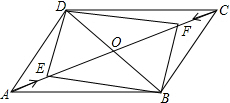 如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?
如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?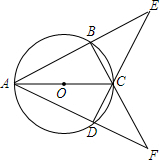 如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.
如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.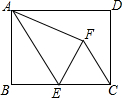 矩形ABCD中,AB=4,BC=6,点E为AB的中点,沿AE将△AEB翻折得到△AFE,sin∠FCE=$\frac{4}{5}$.
矩形ABCD中,AB=4,BC=6,点E为AB的中点,沿AE将△AEB翻折得到△AFE,sin∠FCE=$\frac{4}{5}$.