题目内容
15.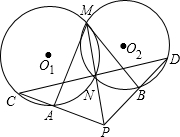 如图,已知⊙O1与⊙O2交于点M,N,MA是⊙O1的切线与⊙O2交于点A,MB是⊙O1的切线与⊙O2交于点B,延长线到点P,使MN=NP,PA与⊙O1交于点C,PB与⊙O2交于点D,求证:C、N、D三点共线,且CN=ND.
如图,已知⊙O1与⊙O2交于点M,N,MA是⊙O1的切线与⊙O2交于点A,MB是⊙O1的切线与⊙O2交于点B,延长线到点P,使MN=NP,PA与⊙O1交于点C,PB与⊙O2交于点D,求证:C、N、D三点共线,且CN=ND.
分析 连接AB、NA、BN、MC.由△MAN∽△BMN,推出$\frac{MA}{MB}$=$\frac{MN}{BN}$,因为MN=NP,推出$\frac{MA}{MB}$=$\frac{NP}{BN}$,即$\frac{NP}{MA}$=$\frac{NB}{MB}$,推出△PNB∽△AMB,推出∠NPB=∠MAB,推出A、P、B、M四点共圆,推出∠MAP=∠MBD=∠MND,因为∠CAM=∠CNM,∠CAM+∠MAP=180°,推出∠CNM+∠MND=180°,推出C、N、D三点共线,再证明△MCN≌△PDN,即可解决问题.
解答 证明:连接AB、NA、BN、MC.
∵MA是⊙O1的切线,MB是⊙O1的切线,
∴∠MAN=∠BMN,∠AMN=∠MBN,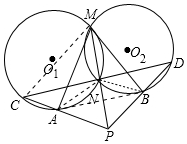
∴△MAN∽△BMN,
∴$\frac{MA}{MB}$=$\frac{MN}{BN}$,
∵MN=NP,
∴$\frac{MA}{MB}$=$\frac{NP}{BN}$,
∴$\frac{NP}{MA}$=$\frac{NB}{MB}$,
∵∠PNB=∠MBN+∠BMN=∠AMN+∠BMN=∠AMB,
∴△PNB∽△AMB,
∴∠NPB=∠MAB,
∴A、P、B、M四点共圆,
∴∠MAP=∠MBD=∠MND,
∵∠CAM=∠CNM,∠CAM+∠MAP=180°,
∴∠CNM+∠MND=180°,
∴C、N、D三点共线,
∵∠MCN=∠PMB=∠NDB,
在△MCN和△PDN中,
$\left\{\begin{array}{l}{∠MCN=∠PDN}\\{∠MNC=∠PND}\\{MN=PN}\end{array}\right.$,
∴△MCN≌△PDN,
∴CN=DN,
∴C、N、D三点共线,且CN=ND.
点评 本题考查圆综合题、切线的性质、全等三角形的判定和性质、相似三角形的判定和性质、四点共圆等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,本题的难点是证明A、P、B、M四点共圆,属于中考压轴题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案| A. | m>4 | B. | m<4 | C. | m≥4 | D. | m≤4 |
| A. | a12=( )3 | B. | a12=( )4 | C. | a12=( )2 | D. | a12=( )6 |
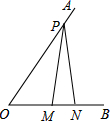 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,若MN=2,则△POM的面积为15$\sqrt{3}$.
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,若MN=2,则△POM的面积为15$\sqrt{3}$.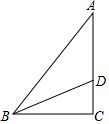 如图:Rt△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,且CD=5,则AD的长为10.
如图:Rt△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,且CD=5,则AD的长为10.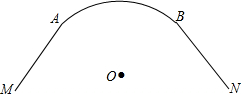 由圆弧形弯道$\widehat{AB}$和两段直道AM、BN组成的一条公路示意图如图所示,直线AM、BN分别与$\widehat{AB}$所在的⊙O相切于点A、B.已知⊙O的半径为90m,$\widehat{AB}$的长为60πm,求直线AM与BN所成的锐角的度数,以及AM,BN的交点到⊙O的切线长.
由圆弧形弯道$\widehat{AB}$和两段直道AM、BN组成的一条公路示意图如图所示,直线AM、BN分别与$\widehat{AB}$所在的⊙O相切于点A、B.已知⊙O的半径为90m,$\widehat{AB}$的长为60πm,求直线AM与BN所成的锐角的度数,以及AM,BN的交点到⊙O的切线长.