题目内容
20.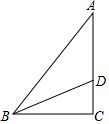 如图:Rt△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,且CD=5,则AD的长为10.
如图:Rt△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,且CD=5,则AD的长为10.
分析 根据∠C=90°,∠A=30°,易求∠ABC=60°,而BD是角平分线,易得∠ABD=∠DBC=30°,那么易证△ABD是等腰三角形,且△BCD是含有30°角的直角三角形,易求BD,从而可求AD.
解答 解:∵∠C=90°,∠A=30°,
∴∠ABC=60°,
又∵BD是角平分线,
∴∠ABD=∠DBC=30°,
在Rt△BCD中,BD=2CD=10,
又∵∠A=∠ABD=30°,
∴AD=BD=10.
故答案为10.
点评 本题考查了直角三角形30°的角所对的边等于斜边的一半的性质,等腰三角形的判定与性质,角平分线定义.解题的关键是求出BD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.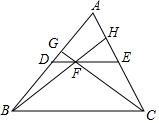 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )| A. | 1:10 | B. | 1:5 | C. | 3:10 | D. | 2:5 |
10.已知⊙O的半径为$\sqrt{3}$,点P到圆心O的距离为2,则点P与⊙O的位置关系是( )
| A. | 点P在⊙O外 | B. | 点P在⊙O上 | C. | 点P在⊙O内 | D. | 无法确定 |
 如图,三个全等的小矩形沿“橫-竖-橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于672cm.
如图,三个全等的小矩形沿“橫-竖-橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于672cm.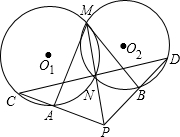 如图,已知⊙O1与⊙O2交于点M,N,MA是⊙O1的切线与⊙O2交于点A,MB是⊙O1的切线与⊙O2交于点B,延长线到点P,使MN=NP,PA与⊙O1交于点C,PB与⊙O2交于点D,求证:C、N、D三点共线,且CN=ND.
如图,已知⊙O1与⊙O2交于点M,N,MA是⊙O1的切线与⊙O2交于点A,MB是⊙O1的切线与⊙O2交于点B,延长线到点P,使MN=NP,PA与⊙O1交于点C,PB与⊙O2交于点D,求证:C、N、D三点共线,且CN=ND.