题目内容
4.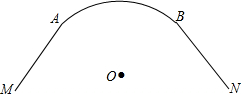 由圆弧形弯道$\widehat{AB}$和两段直道AM、BN组成的一条公路示意图如图所示,直线AM、BN分别与$\widehat{AB}$所在的⊙O相切于点A、B.已知⊙O的半径为90m,$\widehat{AB}$的长为60πm,求直线AM与BN所成的锐角的度数,以及AM,BN的交点到⊙O的切线长.
由圆弧形弯道$\widehat{AB}$和两段直道AM、BN组成的一条公路示意图如图所示,直线AM、BN分别与$\widehat{AB}$所在的⊙O相切于点A、B.已知⊙O的半径为90m,$\widehat{AB}$的长为60πm,求直线AM与BN所成的锐角的度数,以及AM,BN的交点到⊙O的切线长.
分析 作辅助线,由弧长公式求出圆心角为120°,即∠AOB=120°,根据切线的性质得:OA⊥MA,OB⊥BN,则∠CAO=∠CBO=90°,由四边形的内角和为360°求出∠ACB=180°-120°=60°,根据直角三角形30°的三角函数求出结论.
解答 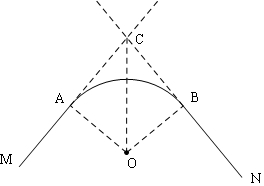 解:连接OA、OB,
解:连接OA、OB,
延长MA、NB交于C,
由弧长公式得:60π=$\frac{∠AOB•90π}{180}$,
∴∠AOB=120°,
∵MA、NB为⊙O的切线,
∴OA⊥MA,OB⊥BN,
∴∠CAO=∠CBO=90°,
∴∠ACB=180°-120°=60°,
∴直线AM与BN所成的锐角的度数为60°,
∴∠AOC=$\frac{1}{2}$∠AOB=60°,
在Rt△AOC中,∠ACO=30°,
∴tan30°=$\frac{OA}{AC}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{90}{AC}$=$\frac{\sqrt{3}}{3}$,
∴AC=90$\sqrt{3}$m,
则AM,BN的交点到⊙O的切线长为90$\sqrt{3}$m.
点评 本题考查了切线的性质和弧长公式、四边形的内角和、特殊角的三角函数值,熟练掌握弧长公式和特殊角的三角函数值是本题的关键,本题虽然难度不大,但应用的知识点较多.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
13.若x>y,则下列式子错误的是( )
| A. | x-1>y-1 | B. | $\frac{x}{3}$>$\frac{y}{3}$ | C. | x+1>y+1 | D. | -3x>-3y |
19.七年级学生计划乘客车去春游,如果减少一辆客车,每辆车正好坐60人,如果增加一辆客车,每辆正好坐45人,则七年级共有学生( )
| A. | 240人 | B. | 360人 | C. | 380人 | D. | 420人 |
16.下列运算正确的是( )
| A. | 8x9÷4x3=2x6 | B. | 4a2b3÷4a2b3=0 | C. | a2m÷am=a2 | D. | 2a2b÷(-$\frac{1}{2}$ab2)=-4c |
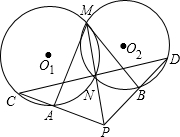 如图,已知⊙O1与⊙O2交于点M,N,MA是⊙O1的切线与⊙O2交于点A,MB是⊙O1的切线与⊙O2交于点B,延长线到点P,使MN=NP,PA与⊙O1交于点C,PB与⊙O2交于点D,求证:C、N、D三点共线,且CN=ND.
如图,已知⊙O1与⊙O2交于点M,N,MA是⊙O1的切线与⊙O2交于点A,MB是⊙O1的切线与⊙O2交于点B,延长线到点P,使MN=NP,PA与⊙O1交于点C,PB与⊙O2交于点D,求证:C、N、D三点共线,且CN=ND.