题目内容
5．关于x的一元二次方程x2-4x+m=0有两个实数根，则实数m的取值范围为（ ）| A． | m＞4 | B． | m＜4 | C． | m≥4 | D． | m≤4 |
分析 根据方程有实数根，得出△≥0，建立关于m的不等式，求出m的取值范围即可．
解答 解：∵关于x的一元二次方程x2-4x+m=0有两个实数根，
∴△≥0，
∴△=16-4m≥0，即m≤4，
故选D．
点评 此题考查了根的判别式，掌握一元二次方程根的情况与判别式△的关系：△＞0?方程有两个不相等的实数根；△=0?方程有两个相等的实数根；△＜0?方程没有实数根是本题的关键．
练习册系列答案
相关题目
16．某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1035张照片，如果全班有x名同学，根据题意，列出方程为（ ）
| A． | x（x+1）=1035 | B． | x（x-1）=1035 | C． | $\frac{1}{2}$x（x+1）=1035 | D． | $\frac{1}{2}$x（x-1）=1035 |
13．若x＞y，则下列式子错误的是（ ）
| A． | x-1＞y-1 | B． | $\frac{x}{3}$＞$\frac{y}{3}$ | C． | x+1＞y+1 | D． | -3x＞-3y |
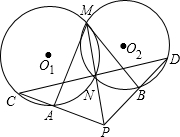如图，已知⊙O1与⊙O2交于点M，N，MA是⊙O1的切线与⊙O2交于点A，MB是⊙O1的切线与⊙O2交于点B，延长线到点P，使MN=NP，PA与⊙O1交于点C，PB与⊙O2交于点D，求证：C、N、D三点共线，且CN=ND．
16．下列运算正确的是（ ）
| A． | 8x9÷4x3=2x6 | B． | 4a2b3÷4a2b3=0 | C． | a2m÷am=a2 | D． | 2a2b÷（-$\frac{1}{2}$ab2）=-4c |