题目内容
8.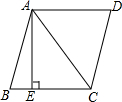 如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则AE的长为$\frac{24}{5}$.
如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则AE的长为$\frac{24}{5}$.
分析 连接BD,根据菱形的性质可得AC⊥BD,AO=$\frac{1}{2}$AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式BC•AE=$\frac{1}{2}$AC•BD可得答案.
解答 解:连接BD,交AC于O点,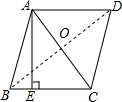
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∴AC⊥BD,AO=$\frac{1}{2}$AC,BD=2BO,
∴∠AOB=90°,
∵AC=6,
∴AO=3,
∴B0=$\sqrt{25-9}$=4,
∴DB=8,
∴菱形ABCD的面积是$\frac{1}{2}$×AC•DB=$\frac{1}{2}$×6×8=24,
∴BC•AE=24,
AE=$\frac{24}{5}$,
故答案为:$\frac{24}{5}$
点评 此题主要考查了菱形的性质,以及菱形的性质面积,关键是掌握菱形的对角线互相垂直且平分.

练习册系列答案
相关题目
18.下列各图中,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
13.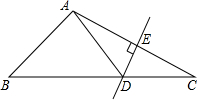 如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为18cm,则△ABC的周长为( )
如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为18cm,则△ABC的周长为( )
 如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为18cm,则△ABC的周长为( )
如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为18cm,则△ABC的周长为( )| A. | 23cm | B. | 28cm | C. | 13cm | D. | 18cm |
17.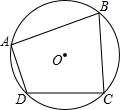 如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )
如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )
 如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )
如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
 已知直线y=$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.
已知直线y=$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.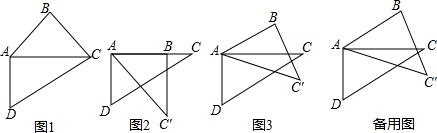
 MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.