题目内容
3.解下列不等式(组)并把它的解集表示在数轴上.(1)10-4(x-3)≤2(x-1)
(2)$\left\{\begin{array}{l}{2x-1<x+1}\\{4x+1>2x-7}\end{array}\right.$.
分析 (1)通过去括号、移项、合并得-6x≤-24,然后把x的系数化为1即可得到不等式的解集,再用数轴表示出解集;
(2)分别解两个不等式得x<2和x>-4,然后根据大小小大中间找确定不等式组的解集,再利用数轴表示解集.
解答 解:(1)去括号得10-4x+12≤2x-2,
移项得-4x-2x≤-2-10-12,
合并得-6x≤-24,
系数化为1得x≥4,
用数轴表示为:
(2)$\left\{\begin{array}{l}{2x-1<x+1①}\\{4x+1>2x-7②}\end{array}\right.$
解①得x<2,
解②得x>-4,
所以不等式组的解集为-4<x<2,
用数轴表示为:
点评 本题考查了解一元一次不等式组:一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.如果a>b,那么下列各式中正确的是( )
| A. | a-2<b-2 | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | -2a<-2b | D. | -a>-b |
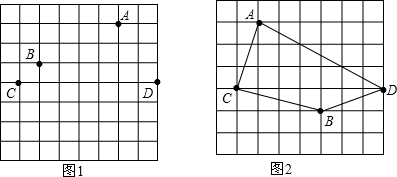
 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )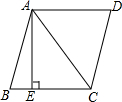 如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则AE的长为$\frac{24}{5}$.
如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则AE的长为$\frac{24}{5}$. 如图,Rt△ABC中,∠ACB=90°,BD是∠ABC的角平分线,AC=8,DC=$\frac{1}{2}$AD,则D到AB的距离为$\frac{8}{3}$.
如图,Rt△ABC中,∠ACB=90°,BD是∠ABC的角平分线,AC=8,DC=$\frac{1}{2}$AD,则D到AB的距离为$\frac{8}{3}$.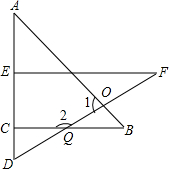 如图,△ABC与△DEF是一副具有一个内角分别为45°和30°直角三角板的拼图,A、E、C、D在同一条线上.
如图,△ABC与△DEF是一副具有一个内角分别为45°和30°直角三角板的拼图,A、E、C、D在同一条线上.