题目内容
如图，在△ABC中，己知∠ACB=90°，CD⊥AB于D．若AD=8，BD=2，则AC=考点：相似三角形的判定与性质
专题：
分析：首先求得AB的长，然后根据△ADC∽△ACB，相似三角形的对应边的比相等，即可求解．
解答：解：∵AD=8，BD=2，
∴AB=AD+BD=10，
∵在△ABC中，∠ACB=90°，CD⊥AB于D，
∴△ADC∽△ACB，
∴
=
，即
=
，
∴AC=4
．
故答案是：4
．
∴AB=AD+BD=10，
∵在△ABC中，∠ACB=90°，CD⊥AB于D，
∴△ADC∽△ACB，
∴
| AD |
| AC |
| AC |
| AB |
| 8 |
| AC |
| AC |
| 10 |
∴AC=4
| 5 |
故答案是：4
| 5 |
点评：本题考查了相似三角形的判定与性质，正确得到△ADC∽△ACB是关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
如图，在正方形网格中，△ABC的顶点都在格点上，则cos∠ABC的值为下列图形中，不一定是轴对称图形的是（ ）
| A、等腰三角形 | B、直角三角形 |
| C、线段 | D、直角 |
下列式子一定成立的是（ ）
| A、3x2-x2=3 |
| B、3a2+2a3=5a5 |
| C、3+x=3x |
| D、-6ab+6ab=0 |
方程x2-4x-6=0的根的情况是（ ）
| A、有两个相等实根 |
| B、有两个不等实根 |
| C、没有实根 |
| D、以上答案都有可能 |
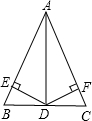如图，在△ABC中，AB=AC，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，则下列说法：①DA平分∠EDF；②AE=AF，DE=DF；③AD上任意一点到B、C两点的距离相等；④图中共有3对全等三角形，其中正确的有（ ）