题目内容
14.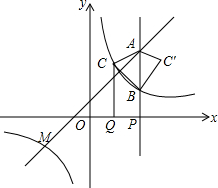 如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.
如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.(1)求反比例函数表达式;
(2)点P是x轴正半轴上的一个动点,设OP=a(a≠2),过点P作垂直于x轴的直线,分别交一次函数,反比例函数的图象于点A,B,过OP的中点Q作x轴的垂线,交反比例函数的图象于点C,△ABC′与△ABC关于直线AB对称.
①当a=4时,求△ABC′的面积;
②当a的值为3时,△AMC与△AMC′的面积相等.
分析 (1)由一次函数解析式可得点M的坐标为(-3,-2),然后把点M的坐标代入反比例函数解析式,求得k的值,可得反比例函数表达式;
(2)①连接CC′交AB于点D.由轴对称的性质,可知AB垂直平分OC′,当a=4时,利用函数解析式可分别求出点A、B、C、D的坐标,于是可得AB和CD的长度,即可求得△ABC的面积;
②由题意得点C的坐标为($\frac{a}{2}$,$\frac{12}{a}$),则C′($\frac{3a}{2}$,$\frac{12}{a}$),根据△AMC与△AMC′的面积相等得出C和C′到直线MA的距离相等,得出C、A、C′三点共线,进而求解.
解答 解:(1)把M(-3,m)代入y=x+1,则m=-2.
将(-3,-2)代入y=$\frac{k}{x}$,得k=6,则反比例函数解析式是:y=$\frac{6}{x}$;
(2)①连接CC′交AB于点D.则AB垂直平分CC′.
当a=4时,A(4,5),B(4,1.5),则AB=3.5.
∵点Q为OP的中点,
∴Q(2,0),
∴C(2,3),则D(4,3),
∴CD=2,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×3.5×2=3.5,则S△ABC′=3.5;
②∵△AMC与△AMC′的面积相等,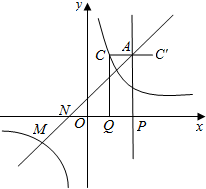
∴C和C′到直线MA的距离相等,
∴C、A、C′三点共线,
∴AP=CQ=$\frac{12}{a}$,
又∵AP=PN,
∴$\frac{12}{a}$=a+1,解得a=3或a=-4(舍去),
∴当a的值为3时,△AMC与△AMC′的面积相等.
故答案是:3.
点评 本题综合考查了待定系数法求函数解析式,函数图象上点的坐标特征以及轴对称的性质.难度较大,解题时需要注意数形结合.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
5.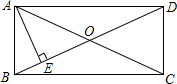 如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )
如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )
 如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )
如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )| A. | 67.5° | B. | 45° | C. | 22.5° | D. | 无法确定 |
 在平面直角坐标系xOy中,一次函数的图象经过点A(1,-3)和B(2,0).
在平面直角坐标系xOy中,一次函数的图象经过点A(1,-3)和B(2,0).