题目内容
4. 在平面直角坐标系xOy中,一次函数的图象经过点A(1,-3)和B(2,0).
在平面直角坐标系xOy中,一次函数的图象经过点A(1,-3)和B(2,0).(1)求这个一次函数的解析式;
(2)若以O、A、B、C为顶点的四边形为菱形,则点C的坐标为(1,3)(直接写出答案).
分析 (1)利用待定系数法求一次函数解析式;
(2)由于AO=AB,于是可判断菱形为OABC,再根据菱形的性质得点C与点A关于y轴对称,然后根据关于y轴对称的点的坐标特征写出C点坐标.
解答 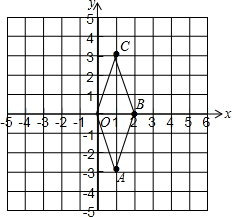 解:(1)设一次函数解析式为y=kx+b,
解:(1)设一次函数解析式为y=kx+b,
把A(1,-3)、B(2,0)代入得$\left\{\begin{array}{l}{k+b=-3}\\{2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-6}\end{array}\right.$,
所以一次函数解析式为y=3x-6;
(2)如图,因为OA=AB,
所以以O、A、B、C为顶点的菱形的对角线为OB和AC,
因为OB与AC互相垂直平分,
所以点C与点A关于y轴对称,
所以C点坐标为(1,3).
故答案为(1,3).
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了待定系数法求一次函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.点P(-2,1)向下平移2个单位长度后,在x轴反射下的像点P′的坐标为( )
| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
12. 矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
 矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
19.在日常生活中如取款、上网都需要密码,有一种用“因式分解法”产生的密码方便记忆,例如,对于多项式x4-y4,因式分解的结果是(x-y)(x+y)(x2+y2).若取x=9,y=9时,则各个因式的值为(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码,对于多项式x3-xy2,取x=20,y=10,用上述方法产生的密码不可能是( )
| A. | 201030 | B. | 201010 | C. | 301020 | D. | 203010 |
9.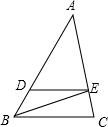 如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
 如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )| A. | 65° | B. | 55° | C. | 45° | D. | 75° |
13.在“走基层,树新风”活动中,青年记者深入边远山区,随机走访农户,调查农村儿童生活教育现状.根据收集的数据,编制了不完整的统计图表如下:
山区儿童生活教育现状
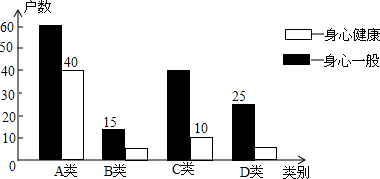
请你用学过的统计知识,解决问题:
(1)记者走访了边远山区多少家农户?
(2)将统计表中的空缺数据填写完整;
(3)分析数据后,你能得出什么结论?
山区儿童生活教育现状
| 类别 | 现状 | 户数 | 比例 |
| A类 | 父母常年在外打工,孩子留在老家由老人照顾 | 100 | |
| B类 | 父母常年在外打工,孩子带在身边 | 20 | 10% |
| C类 | 父母就近在城镇打工,晚上回家照顾孩子 | 50 | |
| D类 | 父母在家务农,并照顾孩子 | 15% |

请你用学过的统计知识,解决问题:
(1)记者走访了边远山区多少家农户?
(2)将统计表中的空缺数据填写完整;
(3)分析数据后,你能得出什么结论?
 如图,在一坡比为1:3的斜坡上种有两棵小树,它们之间的距离AB为10米,则这两棵树的高度差BC为$\sqrt{10}$米.
如图,在一坡比为1:3的斜坡上种有两棵小树,它们之间的距离AB为10米,则这两棵树的高度差BC为$\sqrt{10}$米.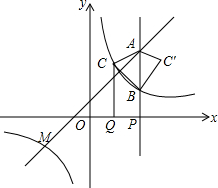 如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.
如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.